
分析 (1)先把各二次根式化为最简二次根式,根据零指数幂计算,然后合并即可.
(2)利用除法法则变形,约分得到最简结果,然后x的值代入计算即可求出值.
解答 解:(1)原式=$\sqrt{2}$+1-4$\sqrt{2}$
=1-3$\sqrt{2}$;
(2)原式=$\frac{x(x-2)}{x+3}$•$\frac{(x+3)^{2}}{x(x+2)(x-2)}$=$\frac{x+3}{x+2}$;
当x=$\sqrt{2}$-2时,原式=$\frac{\sqrt{2}+1}{\sqrt{2}}$=1+$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:填空题
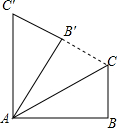 如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.
如图,在△ABC中,∠B=90°,将△ABC绕点A旋转至△AB′C′的位置,若AC′∥BC,C′B′的延长线过点C,则∠BAC的度数为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.
如图,直线y=-x+3与x轴,y轴分别相交于点B,点C,经过B,C两点的抛物线y=ax2+bx+c与x轴的另一交点为A,顶点为P,且对称轴是直线x=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
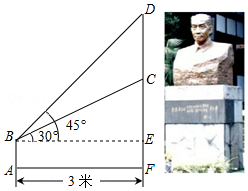 如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7)
如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线y=mx(m为常数,且m≠0)与双曲线y=$\frac{k}{x}$(k为常数,且k≠0)相交于A(-2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为12.
如图,直线y=mx(m为常数,且m≠0)与双曲线y=$\frac{k}{x}$(k为常数,且k≠0)相交于A(-2,6),B两点,过点B作BC⊥x轴于点C,连接AC,则△ABC的面积为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com