
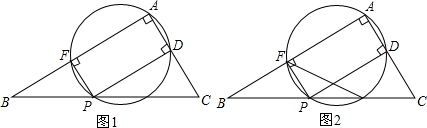
分析 (1)连结FD,AP,它们相交于点O,如图1,先证明四边形ADPF为矩形,则∠FPD=90°,则根据圆周角定理得到点P、F、D在以点O为圆心,OP为半径的圆上,接着根据矩形的性质得OA=OP,然后根据点与圆的位置关系可判断点A在⊙O上;
(2)利用含30度的直角三角形三边的关系得到PF=$\frac{1}{2}$PB=$\frac{1}{2}$x,PD=$\frac{\sqrt{3}}{2}$(4-x),根据正方形的判定方法得$\frac{1}{2}$x=$\frac{\sqrt{3}}{2}$(4-x),解得x=6-2$\sqrt{3}$;
(3)连结AM、AP,作FH⊥BC于H,如图2,先计算出PF=$\frac{1}{2}$x,BF=$\sqrt{3}$PF=$\frac{\sqrt{3}}{2}$x,在Rt△BHF中计算出FH=$\frac{1}{2}$BF=$\frac{\sqrt{3}}{4}$x,在Rt△ABC中计算出AC=$\frac{1}{2}$BC=2,再根据圆周角定理可得到∠AMP=90°,则在Rt△AMC可计算出CM=1,分类讨论:当0<x≤3时,PM=3-x,根据三角形面积公式得到S△PMF=$\frac{1}{2}$•$\frac{\sqrt{3}}{4}$x•(3-x)=-$\frac{\sqrt{3}}{8}$(x-$\frac{3}{2}$)2+$\frac{9\sqrt{3}}{32}$,利用二次函数的性质得x=$\frac{3}{2}$时,S△PMF的最大值为$\frac{9\sqrt{3}}{32}$,当3<x≤4时,PM=x-3,则S△PMF=$\frac{1}{2}$•$\frac{\sqrt{3}}{4}$x•(x-3)=$\frac{\sqrt{3}}{8}$(x-$\frac{3}{2}$)2-$\frac{9\sqrt{3}}{32}$,根据二次函数的性质得x=4时,S△PMF有最大值,最大值为$\frac{\sqrt{3}}{2}$,于是得到△PMF面积的最大值为$\frac{\sqrt{3}}{2}$.
解答 解:(1)连结FD,AP,它们相交于点O,如图1,
∵PF⊥AB,PD⊥AC,
而∠BAC=90°,
∴四边形ADPF为矩形,
∴∠FPD=90°,
∴点P、F、D在以点O为圆心,OP为半径的圆上,
∵OA=OP,
∴点A在⊙O上;
(2)∵∠BAC=90°,∠ABC=30°,
∴∠C=60°,
在Rt△BPF中,∵∠B=30°,
∴PF=$\frac{1}{2}$PB=$\frac{1}{2}$x,
在Rt△PCD中,∵sin∠C=$\frac{PD}{PC}$,
∴PD=(4-x)sin60°=$\frac{\sqrt{3}}{2}$(4-x),
∵四边形ADPF为矩形,
∴当PF=PD时,四边形ADPF为正方形,
即$\frac{1}{2}$x=$\frac{\sqrt{3}}{2}$(4-x),解得x=6-2$\sqrt{3}$,
∴当x等于(6-2$\sqrt{3}$)时,四边形AFPD是正方形;
(3)连结AM、AP,作FH⊥BC于H,如图2,
在Rt△BPF中,∵∠B=30°,
∴PF=$\frac{1}{2}$x,
∴BF=$\sqrt{3}$PF=$\frac{\sqrt{3}}{2}$x,
在Rt△BHF中,FH=$\frac{1}{2}$BF=$\frac{\sqrt{3}}{4}$x,
在Rt△ABC中,∵∠ABC=30°,
∴AC=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2,
∵∠ADP=90°,
∴AP为⊙O的直径,
∴∠AMP=90°,
在Rt△AMC,∵cos∠C=$\frac{MC}{AC}$,
∴CM=2×$\frac{1}{2}$=1,
当0<x≤3时,PM=BC-BP-MC=4-x-1=3-x,
S△PMF=$\frac{1}{2}$•$\frac{\sqrt{3}}{4}$x•(3-x)
=-$\frac{\sqrt{3}}{8}$x2+$\frac{3\sqrt{3}}{8}$x
=-$\frac{\sqrt{3}}{8}$(x-$\frac{3}{2}$)2+$\frac{9\sqrt{3}}{32}$,
x=$\frac{3}{2}$时,S△PMF有最大值,最大值为$\frac{9\sqrt{3}}{32}$,
当3<x≤4时,PM=x-3,
S△PMF=$\frac{1}{2}$•$\frac{\sqrt{3}}{4}$x•(x-3)
=$\frac{\sqrt{3}}{8}$x2-$\frac{3\sqrt{3}}{8}$x
=$\frac{\sqrt{3}}{8}$(x-$\frac{3}{2}$)2-$\frac{9\sqrt{3}}{32}$,
x=4时,S△PMF有最大值,最大值为$\frac{\sqrt{3}}{2}$,
∴△PMF面积的最大值为$\frac{\sqrt{3}}{2}$.
点评 本题考查了圆的综合题:熟练掌握正方形的判定、点与圆的位置关系和圆周角定理;会运用含30度的直角三角形三边的关系计算相应线段的长;会运用二次函数的性质解决最值问题.


科目:初中数学 来源: 题型:填空题
 规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为(-1,-3),如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为(-3,-3).
规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为(-1,-3),如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为(-3,-3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
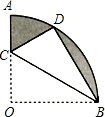 如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,半径OA=6,将扇形AOB沿过点B的直线折叠,点O恰好落在弧AB上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
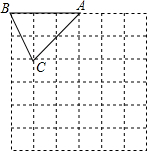 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1.
如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上.将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
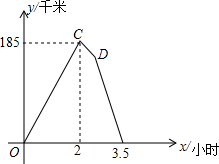 下面的图象反映的过程是:
下面的图象反映的过程是:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是$\sqrt{3}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.瞭望台PC正前方水面上有两艘渔船M,N,观察员在瞭望台顶端P处观测渔船M的俯角α=31°,观测渔船N的俯角β=45°.已知MN所在直线与PC所在直线垂直,垂足为点E,PE长为30米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com