
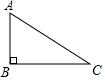
 如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( )
如图,Rt△ABC中,∠ABC=90°,AB=3,BC=6,以AB为边作△ABD,使△ABD与△ABC相似,则在△ABC所在的平面内共存在这样的点D(不与C重合)共有( )| A. | 7个 | B. | 9个 | C. | 11个 | D. | 12个 |
分析 先计算直角三角形两直角边的比为1:2,分五种情况画图:
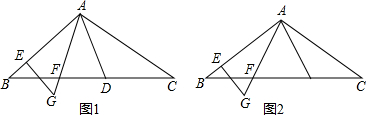
①如图1,BD:AB=1:2时,有两个D点,此时AB与BC对应;
②如图2和图5是与△ABC相似比为1时,有3个D点;
③如图3,AD:AB=1:2时,有两个D点,此时AB与BC对应;
④如图4,根据直径所对的圆周角为直角,以AB为直径画圆,圆周上有4个D点.
解答 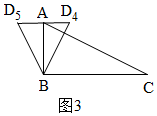

 解:∵AB=3,BC=6,
解:∵AB=3,BC=6,
∴$\frac{AB}{BC}=\frac{3}{6}$=$\frac{1}{2}$,
①当△ABD∽△CBA时,如图1,BD1=BD2=$\frac{3}{2}$,则$\frac{BD}{AB}=\frac{1}{2}$,
存在2个D点;
②当△ABD∽△ABC时,且相似比为1,如图2,存在1个D点;
③当△ABD∽△BCA时,如图3,AD4=AD5=$\frac{3}{2}$,则$\frac{AD}{AB}=\frac{1}{2}$,
存在2个D点;
④以AB为直径作圆,与AC交于D9,连接BD9,过B作BD7⊥BD9,交圆于D7,同理可得D6和D8;
此时△ABD∽△CAB,存在4个D点;
⑤当△ABD∽△BAC时,且相似比为1,如图5,存在2个D点;
综上所述,在△ABC所在的平面内共存在这样的点D(不与C重合)共有11个,
故选C.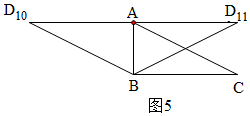
点评 本题考查了直角三角形相似的判定、圆周角定理,熟练掌握直角三角形的判定方法是关键,采用分类讨论的思想,做到不重不漏.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$=±3 | B. | 2a+3b=5ab | C. | (a-b)2=a2-b2 | D. | (-3ab2)2=9a2b4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校有一长方形花圃,里面有一些杂草需要处理.小聪单独完成这项杂草清除任务需要150分钟,小聪单独施工30分钟后,小明加入清理,两人又共同工作了15分钟,完成总清理任务的$\frac{1}{3}$.
某校有一长方形花圃,里面有一些杂草需要处理.小聪单独完成这项杂草清除任务需要150分钟,小聪单独施工30分钟后,小明加入清理,两人又共同工作了15分钟,完成总清理任务的$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com