
| A.不确定 | B.12 | C.11 | D.10 |
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| 34 |
| 34 |
查看答案和解析>>
科目:初中数学 来源: 题型:
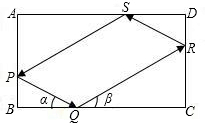
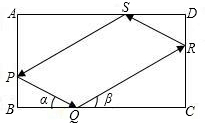 长方形台球桌ABCD上,一球从AB边上某处P击出,分别撞击球桌的边BC、DA各1次后,又回到出发点P处,每次球撞击桌边时,撞击前后的路线与桌边所成的角相等(例如图∠α=∠β)若AB=3,BC=4,则此球所走路线的总长度(不计球的大小)为( )
长方形台球桌ABCD上,一球从AB边上某处P击出,分别撞击球桌的边BC、DA各1次后,又回到出发点P处,每次球撞击桌边时,撞击前后的路线与桌边所成的角相等(例如图∠α=∠β)若AB=3,BC=4,则此球所走路线的总长度(不计球的大小)为( )查看答案和解析>>
科目:初中数学 来源:2011年江苏省无锡市外国语学校中考数学一模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com