
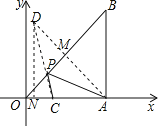
【题目】如图,在平面直角坐标系中,等腰Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(1,0),点P为斜边OB上的一个动点,则PA+PC的最小值为_____.

【答案】![]()
【解析】
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案.
解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,
则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(3,3),
∴AB=3,OA=3,∠B=45°,由勾股定理得:OB=3![]() ,
,
∴AM=![]() OB=
OB=![]() ,
,
∴AD=2AM=3![]() ,
,
∵∠AMB=90°,∠B=45°,
∴∠BAM=45°,
∵∠BAO=90°,
∴∠OAM=45°,
∵DN⊥OA,
∴∠NDA=45°,
∴AN=DN=![]() AD=3
AD=3
∵C(1,0),
∴CN=1,
在Rt△DNC中,由勾股定理得:DC=![]() =
=![]() ,
,
即PA+PC的最小值是![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() 过点A(0,6),点D(8,0),直线
过点A(0,6),点D(8,0),直线![]() :
:![]() 与
与![]() 轴交于点C,两直线
轴交于点C,两直线![]() ,
,![]() 相交于点B.
相交于点B.
(1)求直线![]() 的解析式和点B的坐标;
的解析式和点B的坐标;
(2)连接AC,求![]() 的面积;
的面积;
(3)若在AD上有一点P,把线段AD分成2:3的两部分时,请直接写出点P的坐标(不必写解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)(2015黄石)如图,⊙O的直径AB=4,∠ABC=30°,BC交⊙O于D,D是BC的中点.

(1)求BC的长;
(2)过点D作DE⊥AC,垂足为E,求证:直线DE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1) 如图1,点E为线段AB的中点,连接DE、CE.若AB=4,求线段EC的长
(2) 如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,线段MN与AD交于点G,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论
(3) 在(2)的条件下,若AC=![]() ,请你直接写出DM+CN的最小值
,请你直接写出DM+CN的最小值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王上周五在股市上以收盘价(收市时的价格)每股25元买进某公司股票1 000股,在接下来的一周交易日内,小王记下该股票每日收盘价相比前一天的涨跌情况:(单位:元)

根据上表回答问题:
(1)星期二收盘时,该股票每股______元.
(2)本周内股票收盘时的最高价______元.
(3)已知买入股票与卖出股票均需支付成交金额的千分之五的交易费,若小王在本周五以收盘价将全部股票卖出,他的收益情况如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三点A(-1,1),B(-3,2),C(-4,-1).

(1)作出与△ABC关于原点对称的△A1B1C1,并写出各顶点的坐标;
(2)作出与△ABC关于P(1,-2)点对称的△A2B2C2,并写出各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,再解决问题:
学习数轴之后,有同学发现在数轴上到两点之间距离相等的点,可以用表示这两点表示的数来确定.如:(1)到表示数4和数10距离相等的点表示的数是7,有这样的关系7=![]() (4+10);
(4+10);
(2)到表示数-3和数-7距离相等的点表示的数是-5,有这样的关系-5=![]() .
.
解决问题:根据上述规律完成下列各题:
(1)到表示数50和数150距离相等的点表示的数是_________
(2)到表示数![]() 和数
和数![]() 距离相等的点表示的数是__________
距离相等的点表示的数是__________
(3)到表示数![]() 12和数
12和数![]() 26距离相等的点表示的数是_________
26距离相等的点表示的数是_________
(4)到表示数a和数b距离相等的点表示的数是___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com