
【题目】用适当的方法解方程:
(1)25 y 2- 16 = 0; (2)y 2+ 2 y-99=0;
(3)3x 2 + 2x -3=0; (4)(2x + 1)2 =3(2x + 1).
【答案】(1) y 1 = ![]() y 2= -
y 2= -![]() ; (2) y 1= 9 y2= -11;(3) x 1 =
; (2) y 1= 9 y2= -11;(3) x 1 = ![]() x 2=
x 2=![]() ; (4) x 1= 1 x 2= -
; (4) x 1= 1 x 2= -![]() .
.
【解析】
(1)利用直接开平方法解出方程;
(2)利用配方法解出方程;
(3)利用公式法解出方程;
(4)先把方程化为一般形式,再利用因式分解法解出方程.
(1)25 y 2- 16 = 0
y2=![]()
y=![]() ;
;
(2) y 2+ 2 y-99=0
y 2+ 2 y+1=100
![]()
![]()
y1=9或y2=-11
(3) 3x 2 + 2x -3=0
![]()
x 1 = ![]() x 2=
x 2=![]()
(4) (2x + 1)2 =3(2x + 1)
4x2+4x+1=6x+3
4x2-2x-2=0
(4x+2)(x-1)=0
x 1= 1 x 2= -![]()


科目:初中数学 来源: 题型:
【题目】已知点O是等腰直角三角形ABC斜边上的中点,AB=BC,E是AC上一点,连结EB.
(1) 如图1,若点E在线段AC上,过点A作AM⊥BE,垂足为M,交BO于点F.求证:OE=OF;
(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交OB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,AB=10,BD=4,BE=2,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD的右侧按如图所示的方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB经过x轴上的点A(2,0),且与抛物线相交于B、C两点,已知B点坐标为(1,1) .
(1)求直线和抛物线的解析式;
(2)如果D为抛物线上一点,使得△AOD与△OBC的面积相等,求D点坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
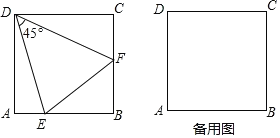
【题目】如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45°,交直线BC边于点F,连结EF.
探究:当点E在边AB上,求证:EF=AE+CF.
应用:(1)当点E在边AB上,且AD=2时,则△BEF的周长是______.
(2)当点E不在边AB上时,EF,AE,CF三者的数量关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜀山区植物园是一座三面环水的半岛园区,拥有梅园、桂花园、竹园、木兰园、水景园等示范区。为了种植植物,需要从甲乙两地向园区A,B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A,B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需费用)。
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
运往A、B两地的吨数 | ||
A | B | |
甲地 | x | 50-x |
乙地 | ( ) | ( ) |
(1)设甲地运往A棚营养土x吨,请用关于x的代数式完成上表;
(2)设甲地运往A棚营养土x吨,求总运费y(元)关于x(吨)的函数关系式(要求写出变量取值范围);
(3)当甲、乙两地各运往A、B两棚多少吨营养土时,总运费最省?最省的总运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(0,4),线段
的坐标为(0,4),线段![]() 的位置如图所示,其中点
的位置如图所示,其中点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(3,
的坐标为(3,![]() ).
).

(1)将线段![]() 平移得到线段
平移得到线段![]() ,其中点
,其中点![]() 的对应点为
的对应点为![]() ,点
,点![]() 的对应点为点
的对应点为点![]() .
.
①点![]() 平移到点
平移到点![]() 的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
的过程可以是:先向 平移 个单位长度,再向 平移 个单位长度;
②点![]() 的坐标为 .
的坐标为 .
(2)在(1)的条件下,若点![]() 的坐标为(4,0),连接
的坐标为(4,0),连接![]() ,画出图形并求
,画出图形并求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com