
分析 先分子分母因式分解,再通分,把a的值求出来,代入即可.
解答 解:原式=$\frac{2}{a+1}$-$\frac{a-2}{(a+1)(a-1)}$+$\frac{a(a-2)}{(a-1)^{2}}$
=$\frac{2(a-1)^{2}-(a-2)(a-1)+a(a-2)(a+1)}{(a+1)(a-1)^{2}}$
=$\frac{a(2a-3)}{(a+1)(a-1)^{2}}$,
∵a=cos45°,
∴a=$\frac{\sqrt{2}}{2}$,
∴原式=$\frac{\frac{\sqrt{2}}{2}(2×\frac{\sqrt{2}}{2}-3)}{(\frac{\sqrt{2}}{2}+1)(\frac{\sqrt{2}}{2}-1)^{2}}$
=$\frac{2-3\sqrt{2}}{\frac{\sqrt{2}-2}{2}}$
=8$\sqrt{2}$-10.
点评 本题考查了分式的化简求值,以及锐角三角函数,分式的通分、约分以及因式分解是解题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 采购部 | 经理,这里有一批商品以每件42元购回 |
| 销售部 | 经理,以每件42元购回的商品,每天的销售量t(件)与每件的销售价x(元)呈现的关系是:t=-3x+204 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
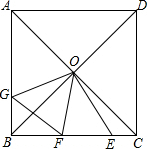 如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F为BC边上的两点,且∠EOF=45°,过点O作OE的垂线OG,交AB于点G,连接FG,下列结论:①△COE≌△BOG;②△COE≌△BOF;③CE+BF>EF;④CE2+BF2=EF2.其中正确的有( )
如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F为BC边上的两点,且∠EOF=45°,过点O作OE的垂线OG,交AB于点G,连接FG,下列结论:①△COE≌△BOG;②△COE≌△BOF;③CE+BF>EF;④CE2+BF2=EF2.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
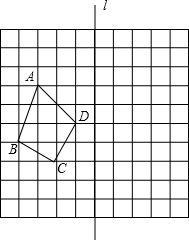 如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.
如图,在由边长为1的小正方形组成的10×10的网格中(我们把组成网格的小正方形的顶点称为格点),四边形ABCD在直线l的左侧,其四个顶点A,B,C,D分别在网格的格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=6时,这两个二次函数的最大值之和等于( )
如图,已知点A(8,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=6时,这两个二次函数的最大值之和等于( )| A. | 5 | B. | $\frac{{8\sqrt{5}}}{3}$ | C. | 10 | D. | $2\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com