练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．2$\frac{7}{8}$比甲数多$\frac{1}{3}$，那么甲数为2$\frac{13}{24}$．

    分析 根据“2$\frac{7}{8}$比甲数多$\frac{1}{3}$，”知道甲数比$2\frac{7}{8}$少$\frac{1}{3}$，所以用$2\frac{7}{8}$-$\frac{1}{3}$就是甲数，再根据分数减法的计算方法，即可得出答案．

    解答 解：$2\frac{7}{8}$-$\frac{1}{3}$=2$\frac{21}{24}$-$\frac{8}{24}$=2$\frac{13}{24}$
    故答案为：$2\frac{13}{24}$．

    点评 解答此题的关键是，弄清题意正确列出算式，再根据异分母分数减法的计算方法作答，即先化成同分母的分数，然后分母不变，只把分子相加减．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．计算：
    （1）$\sqrt{\frac{25}{4}x}$-$\sqrt{9x}$+$\sqrt{16x}$；
    （2）（$\sqrt{3}$-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．计算：（$\sqrt{3}$-1）0+（-$\frac{1}{2}$）-1=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图是一张直角三角形纸片，两直角边AC=6cm，BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．如图，在菱形ABCD中，点E、F分别是AB、AC的中点，如果菱形ABCD的周长是32，那么EF的长为（　　）
    A．4B．8C．28D．32

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．问题：在下面括号里填上适当的自然数，使等式成立． $\frac{1}{6}=\frac{1}{{（{\;}\right.\left.{\;}）}}+$$\frac{1}{{（{\;}\right.\left.{\;}）}}$=$\frac{1}{{（{\;}\right.\left.{\;}）}}$+$\frac{1}{{（{\;}\right.\left.{\;}）}}$=.$\frac{1}{{（{\;}\right.\left.{\;}）}}$+$\frac{1}{{（{\;}\right.\left.{\;}）}}$=$\frac{1}{{（{\;}\right.\left.{\;}）}}$+$\frac{1}{{（{\;}\right.\left.{\;}）}}$=$\frac{1}{{（{\;}\right.\left.{\;}）}}$+$\frac{1}{{（{\;}\right.\left.{\;}）}}$
    分析：把$\frac{1}{6}$表示成两个单位分数（分子为1的分数）的和，可以这样考虑：若两个加数相同，则$\frac{1}{6}=\frac{1×2}{6×2}=\frac{1}{12}+\frac{1}{12}$；
    若两个加数不相同，可利用分数的基本性质将分数的分子、分母扩大相同的倍数，再将分子拆成两个自然数的和，即：
    $\frac{1}{6}=\frac{1×A}{6×A}=\frac{B+C}{6A}=\frac{B}{6A}+\frac{C}{6A}$（A=B+C，A、B、C是自然数），若B、C是6的约数，则$\frac{B}{6A}、\frac{C}{6A}$可以化成单位分数．
    所以$\frac{1}{6}=\frac{1}{12}+\frac{1}{12}=\frac{1}{15}+\frac{1}{10}=\frac{1}{18}+\frac{1}{9}=\frac{1}{24}+\frac{1}{8}=\frac{1}{42}+\frac{1}{7}$；
    根据对上述材料的理解完成下列各题：
    （1）在下面括号里填上相同的自然数，使等式成立$\frac{1}{10}$=$\frac{1}{（\;\;\;）}$+$\frac{1}{（\;\;\;）}$
    （2）已知$\frac{1}{10}$=$\frac{1}{A}+\frac{1}{B}$
    （A、B是不相等的自然数）求所有满足条件A、B的值．（直接写出答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．把抛物线y1向右平移2个单位，再绕原点旋转180°得到抛物线y2=2x2+4x+4，则y1的解析式为y1=-2（x+1）2-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．定义一种法则“⊕”如下：a⊕b=$\left\{\begin{array}{l}{a（a＞b）}\\{b（a≤b）}\end{array}\right.$，例如：1⊕2=2，若（-3p+5）⊕11=11，则p的取值范围是p≥-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

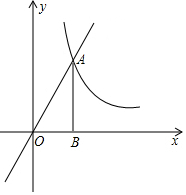    12．已知图中的曲线是反比例函数y=$\frac{m-5}{x}$（m为常数）图象的一支．
    （1）这个反比例函数图象的另一支在第第三象限，常数m的取值范围是m＞5．
    （2）若该函数的图象任取一点A，过A点作x轴的垂线，垂足为B，当△OAB的面积为4时，求反比例函数的解析式．

    查看答案和解析>>

    同步练习册答案