
【题目】如图,![]() 中,
中,![]() ,
,![]() .
.![]() 、
、![]() 是边
是边![]() 、
、![]() 边上的动点,
边上的动点,![]() 从
从![]() 出发向
出发向![]() 运动,同时
运动,同时![]() 以相同的速度从
以相同的速度从![]() 出发向
出发向![]() 运动,
运动,![]() 运动到
运动到![]() 停止.
停止.![]() 为
为![]() 中点.
中点.
![]() 试探究
试探究![]() 的形状,并说明理由.
的形状,并说明理由.
![]() 在运动过程中,四边形
在运动过程中,四边形![]() 可能成为正方形吗?如能求正方形的边长.
可能成为正方形吗?如能求正方形的边长.
![]() 当
当![]() 为多少时,
为多少时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?

【答案】![]() 为等腰直角三角形,理由见解析;
为等腰直角三角形,理由见解析;![]() 四边形
四边形![]() 是正方形,且其边长为
是正方形,且其边长为![]() ;(
;(![]() 为
为![]() 时,
时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .
.
【解析】
(1)根据F是AB中点,可得AF=BF=CF,∠A=∠FCE=45°,即可证明△ADF≌△CEF,于是可得DF=EF,∠AFD=∠CFE,即可求得∠DFE=90°,即可得到结论;
(2)根据三角形中位线定理和等腰直角三角形的性质即可证得;
(3)设AD=x,则CE=x,DC=8-x,根据三角形面积公式得出函数关系式,根据函数的顶点式即可求得.
解:![]() 为等腰直角三角形,
为等腰直角三角形,
理由:如图连接![]() ,
,
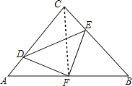
∵![]() 是
是![]() 中点,
中点,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
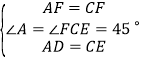 ,
,
∴![]() ;
;
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;![]() 当
当![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点时,四边形
中点时,四边形![]() 是正方形,
是正方形,
∵![]() ,
,![]() 为
为![]() 中点,
中点,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是正方形,且其边长为
是正方形,且其边长为![]() ;
;![]() 设
设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,
∴当![]() 为
为![]() 时,
时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .
.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的“点角距离”,记为d(P,∠MON).如图乙,在平面直角坐标系xOy中,点P在坐标平面内,且点P的横坐标比纵坐标大2,对于∠xOy,满足d(P,∠xOy)=10,点P的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花木公司在20天内销售一批马蹄莲.其中,该公司的鲜花批发部日销售量y1(万朵)与时间x(x为整数,单位:天)部分对应值如下表所示.
时间x(天) | 0 | 4 | 8 | 12 | 16 | 20 |
销量y1(万朵) | 0 | 16 | 24 | 24 | 16 | 0 |
另一部分鲜花在淘宝网销售,网上销售日销售量y2(万朵)与时间x(x为整数,单位:天) 关系如下图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与x的变化规律,写出y1与x的函数关系式及自变量x的取值范围;
(2)观察马蹄莲网上销售量y2与时间x的变化规律,请你设想商家采用了何种销售策略使得销售量发生了变化,并写出销售量y2与x的函数关系式及自变量x的取值范围;
(3)设该花木公司日销售总量为y万朵,写出y与时间x的函数关系式,并判断第几天日销售总量y最大,并求出此时最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是一条高速公路的隧道口在平面直角坐标系上的示意图,点![]() 和
和![]() 、点
、点![]() 和
和![]() 分别关于
分别关于![]() 轴对称,隧道拱部分
轴对称,隧道拱部分![]() 为一条抛物线,最高点
为一条抛物线,最高点![]() 离路面
离路面![]() 的距离为
的距离为![]() 米,点
米,点![]() 离路面为
离路面为![]() 米,隧道的宽度
米,隧道的宽度![]() 为
为![]() 米;则隧道拱抛物线
米;则隧道拱抛物线![]() 的函数解析式________.
的函数解析式________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑公司甲、乙两个工程队通过公开招标获得某改造工程项目.已知甲队单独完成这项工程的时间是乙队单独完成这项工程时间的![]() 倍,由于乙队还有其他任务,先由甲队单独做55天后,再由甲、乙两队合做20天,完成了该项改造工程任务.
倍,由于乙队还有其他任务,先由甲队单独做55天后,再由甲、乙两队合做20天,完成了该项改造工程任务.
(Ⅰ)请根据题意求甲、乙两队单独完成改造工程任务各需多少天;
(Ⅱ)这项改造工程共投资200万元,如果按完成的工程量付款,那么甲、乙两队可获工程款各多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)小龙一共抽取了 名学生.
(2)补全条形统计图;
(3)求“其他”部分对应的扇形圆心角的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com