

���� ��1������ͳ��ͼ��֪��10�֡�15�֡����û�10��ռ10%���Ӷ�������ô˴ε����ȡ�Ļ�����
��2�����ݣ�1������õ��û���������ͳ��ͼ���Եõ���15�֡�20�֡����û����������������ͼ�С�15�֡�20�֡����ֵ�Բ�ĽǵĶ�����
��3������ǰ��ͳ��ͼ����Ϣ���Եõ��õ���40���û���Լ�ж����û�����ˮȫ�����ܻ����۸�
��� �⣺��1��10��10%=100 ������
�𣺹���ȡ��100����
��2��15�֡�20�ֻ���Ϊ��100-10-38-24-8=20��
��ȫƵ���ֲ�ֱ��ͼ���£�
����ͼ�С�15�֡�20�֡����ֵ�Բ�ĽǵĶ���Ϊ$\frac{20}{100}$��360��=72�㣻
��3��40��$\frac{10+20+38}{100}$=27.2����
��Լ��27.2�����ܻ����۸�
���� ���⿼��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ���������������壬����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -8 | B�� | 10 | C�� | -4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
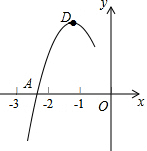 ������y=ax2+bx+c�Ķ���ΪD��-1��2������x���һ������A�ڵ㣨-3��0���ͣ�-2��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���b2-4ac��0����a+b+c��0����2a+b=0����c-a=2����4ac-8a=b2������ax2+bx+c-1=0��������ȵ�ʵ������������ȷ���۵ĸ���Ϊ��������
������y=ax2+bx+c�Ķ���ΪD��-1��2������x���һ������A�ڵ㣨-3��0���ͣ�-2��0��֮�䣬�䲿��ͼ����ͼ��ʾ�������н��ۣ���b2-4ac��0����a+b+c��0����2a+b=0����c-a=2����4ac-8a=b2������ax2+bx+c-1=0��������ȵ�ʵ������������ȷ���۵ĸ���Ϊ��������| A�� | 3�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com