
【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.
【答案】(1)40,12;(2)1200;(3)![]()
【解析】
(1)用赞同D的人数除以对应的百分比即可得到m的值,用总人数乘以赞同B的人对应的百分比即可得出b值;
(2)用赞同A的人对应的百分比乘以人数,即可得出这些大学生中选择赞同A选项的人数;
(3)用树状图法列出所有结果,再计算概率,即可得出答案.
(1)m=20÷50%=40,
b=40×30%=12;
(2)a=40-12-4-20=4,
12000×![]() =1200(人),
=1200(人),
故若该地区18~20岁的大学生有1.2万人,估计这些大学生中选择赞同A选项的人数为1200人;
(3)画树状图如图所示:
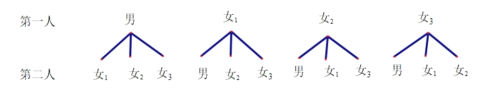
从选“C”的4人中随机抽取2人,有12种等可能的结果,这名男性被抽取到的结果有6种,
∴这名男性被抽取到的概率为![]() =
=![]() .
.


科目:初中数学 来源: 题型:
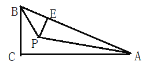
【题目】如图,在△ABC中,∠C=90°,∠A和∠B的平分线交于点P,过点P作PE⊥AB交AB于点E.若BC=5,AC=12,则AE等于______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市平时每天都将一定数量的白糖和红糖进行包装以便出售,已知每天包装白糖的质量是包装红糖质量的![]() 倍,且每天包装白糖和红糖的质量之和为45千克.
倍,且每天包装白糖和红糖的质量之和为45千克.
(1)求平均每天包装白糖和红糖的质量各是多少千克?
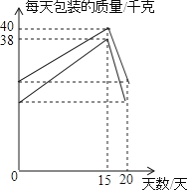
(2)为迎接今年6月25日的“端午节”,该超市决定在前20天增加每天包装白糖和红糖的质量,二者的包装质量与天数的变化情况如图所示,节日后又恢复到原来每天的包装质量.直接写出在这20天内每天包装白糖和红糖的质量随天数变化的函数关系式,并写出自变量的取值范围.
(3)假设该超市每天都会将当天包装后的白糖和红糖全部售出,已知白糖的成本价为每千克3.9元,红糖的成本每千克5.5元,二者包装费用平均每千克均为0.5元,白糖售价为每千克6元,红糖售价为每千克8元,那么在这20天中有哪几天销售白糖和红糖的利润之和大于120元?[总利润=售价额﹣成本﹣包装费用].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数a、b、c满足(a-b)2=ab=c,有下列结论:①当c≠0时,![]() =3;②当c=5时,a+b=5:③当a、b、c中有两个相等时,c=0;④二次函数y=x2+bx-c与一次函数y=ax+1的图象有2个交点.其中正确的有_______
=3;②当c=5时,a+b=5:③当a、b、c中有两个相等时,c=0;④二次函数y=x2+bx-c与一次函数y=ax+1的图象有2个交点.其中正确的有_______
查看答案和解析>>
科目:初中数学 来源: 题型:
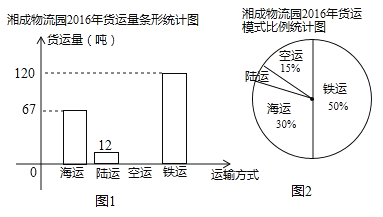
【题目】在“一带一路”倡议下,我国已成为设施联通,贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,如图是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图.
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?并补全条形统计图;
(3)求条形统计图中陆运货物量对应的扇形圆心角的度数?
查看答案和解析>>
科目:初中数学 来源: 题型:
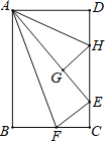
【题目】在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
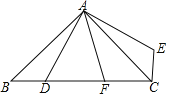
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD≌△ACE;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y1=ax2﹣![]() x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,
x+c与x轴交于点A和点B(1,0),与y轴交于点C(0,![]() ),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
),抛物线y1的顶点为G,GM⊥x轴于点M.将抛物线y1平移后得到顶点为B且对称轴为直线l的抛物线y2.
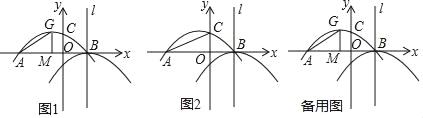
(1)求抛物线y2的解析式;
(2)如图2,在直线l上是否存在点T,使△TAC是等腰三角形?若存在,请求出所有点T的坐标;若不存在,请说明理由;
(3)点P为抛物线y1上一动点,过点P作y轴的平行线交抛物线y2于点Q,点Q关于直线l的对称点为R,若以P,Q,R为顶点的三角形与△AMG全等,求直线PR的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com