练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．已知$\frac{A}{x+1}$-$\frac{B}{x-3}$=$\frac{x+5}{（x+1）（x-3）}$（其中A，B为常数），求A2014B=-2．

    分析 根据分式的加减运算法则列出关于A、B的方程组即可求出A、B的值．

    解答 解：$\frac{A}{x+1}$-$\frac{B}{x-3}$=$\frac{A（x-3）-B（x+1）}{（x+1）（x-3）}$=$\frac{（A-B）x-3A-B}{（x+1）（x-3）}$
    ∴$\left\{\begin{array}{l}{A-B=1}\\{-3A-B=5}\end{array}\right.$
    解得：$\left\{\begin{array}{l}{A=-1}\\{B=-2}\end{array}\right.$
    ∴原式=（-1）2014×（-2）=-2
    故答案为：-2

    点评 本题考查分式的加减法，解题的关键是熟练运用分式的运算法则，本题属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．为测量底面为圆形的古塔的高度，以下是小明与小红的研究报告：
    小明的研究报告小红的研究报告
    测量图例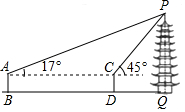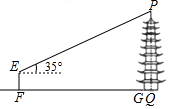
    测量过程如图，测角仪AB、CD的高度均为1.6m，分别测得古塔顶端的仰角为17°、45°，测角仪底端的距离（BD）为69m．如图，测角仪EF的高度为1.6m，测得古塔顶端的仰角为35°，测角仪所在位置与古塔底部边缘的最短距离（FG）为38.3m．
    参考数据sin17°≈0.29，cos17°≈0.96，
    tan17°≈0.31，$\sqrt{2}$≈1.41    		sin35°≈0.57，cos35°≈0.82，
    tan35°≈0.70
    数据处理32.6PQ=38.3×tan35°+1.6≈28.41（m）
    （1）写出小明的研究报告中“数据处理”的详细过程；
    （2）指出小红研究报告中的错误之处；
    （3）利用两人的测量数据，直接写出古塔底面圆的半径（结果精确到1m）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．${（-\frac{2}{3}）}^{-2}$+（π-3.14）0-|-$\frac{1}{4}$|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．“端午节”是中华民族古老的传统节日．甲、乙两家超市在“端午节”当天对一种原来售价相同的粽子分别推出了不同的优惠方案．
    甲超市方案：购买该种粽子超过200元后，超出200元的部分按95%收费；
    乙超市方案：购买该种粽子超过300元后，超出300元的部分按90%收费．
    设某位顾客购买了x元的该种粽子．
    （1）补充表格，填写在“横线”上：
    x
    （单位：元）    		实际在甲超市的花费
    （单位：元）    		实际在乙超市的花费
    （单位：元）
    0＜x≤200xx
    200＜x≤300200+（x-200）×95%（或10+0.95x）x
    x＞300200+（x-200）×95%（或10+0.95x）300+（x-300）×90%（或30+0.9x）
    （2）当x为何值时？到甲、乙两超市的花费一样．
    （3）如果顾客在“端午节”当天购买该种粽子超过300元，那么到哪家超市花费更少？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，现有若干张卡片，分别是正方形卡片A、B和长方形卡片C，卡片大小如图所示．如果要拼一个长为（4a+b），宽为（a+2b）的大长方形，则需要C类卡片9张．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．解方程组：
    （1）$\left\{\begin{array}{l}x-y=1\\ 3（x-y）+2y=5\end{array}$
    （2）$\left\{\begin{array}{l}{11x+12y=13}\\{14x+15y=16}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知a2+2ab-b2=0，且ab≠0，则$\frac{b}{a}$-$\frac{a}{b}$=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在解决“过直线AB外一点P画AB的平行线”的问题时，小明使用了一块三角板来完成作图，他的作法如下：
    第①步：如图①，用三角板的一条直角边贴住直线AB，并且使斜边正好经过点P，沿斜边画直线PQ；
    第②步：用同一块三角板的斜边贴住直线PQ，并使一条直角边经过点P，沿这条直角边画直线CD，则CD∥AB．

    请根据上面的信息，在图②中画出三角板的位置和直线CD，并写出这样画平行线的依据：内错角相等，两直线平行．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解下列方程
    （1）$\frac{6}{x-2}$=$\frac{1}{x+3}$；
    （2）$\frac{x+1}{x-1}$-$\frac{4}{{x}^{2}-1}$=1．

    查看答案和解析>>

    同步练习册答案