
【题目】如图,四边形ABCD是平行四边形,点E、F在BC上,且CF=BE,连接DE,过点F作FG⊥AB于点G.

(1)如图1,若∠B=60°,DE平分∠ADC,且 ![]() ,
,![]() ,求平行四边形ABCD的面积.
,求平行四边形ABCD的面积.
(2)点H在GF上,且HE=HF,延长EH交AC,CD于点O,Q,连接AQ,若AC=BC=EQ,∠EQC=45°,求证:![]() .
.
【答案】(1)18![]() +9;(2)见详解.
+9;(2)见详解.
【解析】
(1)由角平分线的定义及平行四边形的性质,得CD=CE=6,从而得CF=![]() ,进而得BC=6+
,进而得BC=6+![]() .过点A作AM⊥BC于点M,得AM=
.过点A作AM⊥BC于点M,得AM= ![]() ,根据平行四边形的面积公式,即可求解.
,根据平行四边形的面积公式,即可求解.
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,先证△BGF≌△CNE(AAS),再证△ACK≌△QEC(ASA),进而即可得到结论.
(1)∵DE平分∠ADC,
∴∠ADE=∠CDE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADE=∠CED,
∴∠CED=∠CDE,
∴CD=CE=6,
∵![]() ,
,
∴CF=![]() ,
,
∵CF=BE,
∴BE=![]() ,
,
∴BC=6+![]() .
.
过点A作AM⊥BC于点M,
∵∠B=60°,AB=CD=6,
∴∠BAM=30°,
∴BM=3,
∴AM=![]() BM=
BM=![]() ,
,
∴平行四边形ABCD的面积=(6+![]() )×
)×![]() =18
=18![]() +9;
+9;
(2)过点C作CN⊥EQ于点N,其延长线交AD于点K,
∵∠EQC=45°,
∴△CNQ为等腰直角三角形,
∴∠NQC=∠NCQ=45°,且CQ=![]() CN,
CN,
∵HE=HF,
∴∠HEF=∠HFE,
∵FG⊥AB,CN⊥EQ,
∴∠FGB=∠ENC=90°,
又∵BE=CF,
∴BF=CE,
∴△BGF≌△CNE(AAS),
∴BG=CN,∠B=∠ECN,
∴CQ=![]() BG,
BG,
又∵AC=BC=AD,
∴∠D=∠ACD,
又∵∠B=∠D,
∴∠ECN=∠ACD,
∴∠KAC=∠BCA=∠NCQ=45°,
∴∠BAC=∠ACD=∠B=∠CDA=∠ECN =67.5°,
∴∠ACK= ∠ECN-∠BCA =22.5°,∠QEC=180°-90°-∠ECN =22.5°,
即:∠ACK=∠QEC,
又∵∠KAC=∠CQE=45°,AC=QE,
∴△ACK≌△QEC(ASA),
∴CK=CE,
∵∠CDA=67.5°,∠NCQ=45°,
∴∠CKD=180°-45°-67.5°=67.5°,
∴∠CKD=∠CDA,
∴CK=CD,
∴CE=CD,
∵CD=CQ+QD=![]() BG+DQ,
BG+DQ,
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数![]() 的图象上.那么k的值是
的图象上.那么k的值是
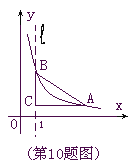
A .3 B.6 C.12 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F是正方形ABCD的边CD上两个动点,满足DE=CF.连接AE交BD于点I,连接BF交CI于点H,G为BC边上的中点.若正方形的边长为4,则线段DH长度的最小值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①所有锐角三角函数值都为正数;②解直角三角形时只需已知除直角外的两个元素;③Rt△ABC中,∠B=90°,则sin2A+cos2A=1;④Rt△ABC中,∠A=90°,则tanCsinC=cosC.其中正确的命题有( )
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某船自西向东航行,在![]() 处测得某岛
处测得某岛![]() 在北偏东
在北偏东![]() 的方向上,前进
的方向上,前进![]() 海里后到达
海里后到达![]() ,此时,测得海岛
,此时,测得海岛![]() 在北偏东
在北偏东![]() 的方向上,要使船与海岛
的方向上,要使船与海岛![]() 最近,则船应继续向东前进________海里.
最近,则船应继续向东前进________海里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了改善办公条件,计划从厂家购买![]() 、
、![]() 两种型号电脑.已知每台
两种型号电脑.已知每台![]() 种型号电脑价格比每台
种型号电脑价格比每台![]() 种型号电脑价格多0.1万元,且用10万元购买
种型号电脑价格多0.1万元,且用10万元购买![]() 种型号电脑的数量与用8万元购买
种型号电脑的数量与用8万元购买![]() 种型号电脑的数量相同.求
种型号电脑的数量相同.求![]() 、
、![]() 两种型号电脑每台价格各为多少万元?
两种型号电脑每台价格各为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
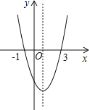
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .其中,正确的说法有________(请写出所有正确说法的序号).
.其中,正确的说法有________(请写出所有正确说法的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com