
【题目】某电子厂商投产一种新型电子产品,每件制造成本为16元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)如果厂商每月的制造成本不超过480万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
【答案】(1)z=﹣2x2+132x﹣1600;(2)当销售单价为35元时,厂商每月获得的利润最大,最大利润为570万元.
【解析】
(1)根据每月的利润z=(x16)×y,再把y=2x+100代入即可求出z与x之间的函数解析式,
(2)先根据制造成本不超过480万元知生产量不超过30万件,结合一次函数解析式得出x的取值范围,把函数关系式变形为顶点式运用二次函数的性质求出最值.
解:(1)根据题意知,z=(x﹣16)(﹣2x+100)=﹣2x2+132x﹣1600;
(2)厂商每月的制造成本不超过480万元,每件制造成本为16元,
∴每月的生产量为:小于等于![]() =30万件,
=30万件,
则y=﹣2x+100≤30,
解得:x≥35,
∵z=﹣2x2+132x﹣1600=﹣2(x﹣33)2+578,
∴图象开口向下,对称轴右侧z随x的增大而减小,
∴x=35时,z最大为570万元.
当销售单价为35元时,厂商每月获得的利润最大,最大利润为570万元.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物BC的高度,他们先在斜坡上的D处,测得建筑物顶端B的仰角为30°.且D离地面的高度DE=5m.坡底EA=30m,然后在A处测得建筑物顶端B的仰角是60°,点E,A,C在同一水平线上,求建筑物BC的高.(结果用含有根号的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-(m+2)x+(2m-1)=0。
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC 中,AB=AC.
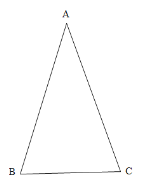
(1)求作△ABC 外接圆(尺规作图)
(2)若△ABC 的外接圆的圆心O到 BC 边的距离为 4,BC=6,求外接圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
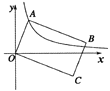
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 在第一象限图像上的一个动点,连接
在第一象限图像上的一个动点,连接![]() ,以
,以![]() 为长,
为长,![]() 为宽作矩形
为宽作矩形![]() ,且点
,且点![]() 在第四象限,随着点
在第四象限,随着点![]() 的运动,点
的运动,点![]() 也随之运动,但点
也随之运动,但点![]() 始终在反比例函数
始终在反比例函数![]() 的图像上,则
的图像上,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
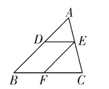
【题目】如图,在△ABC 中,D、E、F 分别为边 AB、AC、BC 上的点,连接 DE、EF.若 DE∥BC,EF∥AB,则图中共有________对相似三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
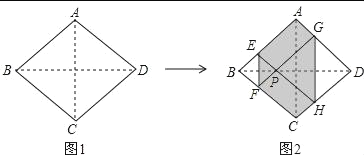
【题目】如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2),设AE=x(0<x<2),给出下列判断:①x=![]() 时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
A.①②B.①③C.②D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC.
(操作)(1)将△ABD绕点D沿顺时针方向旋转60°,在图中画出旋转后的三角形.
(探究)(2)结合所画图形探究BD与AB,BC之间的数量关系,并证明你的结论.
(应用)(3)若AB=6,BC=8,试求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
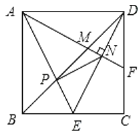
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com