
| 应试者 | 听 | 说 | 读 | 写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
分析 (1)根据平均数的计算公式计算可得;
(2)根据加权平均数的公式计算可得.
解答 解:(1)∵$\overline{{x}_{甲}}$=$\frac{1}{4}$×(85+78+85+73)=80.25,$\overline{{x}_{乙}}$=$\frac{1}{4}$×(73+80+82+83)=79.5,
∴应录取甲;
(2)∵$\overline{{x}_{甲}}$=$\frac{85×2+78×1+85×3+73×4}{2+1+3+4}$=79.5,$\overline{{x}_{乙}}$=$\frac{73×2+80×1+82×3+83×4}{2+1+3+4}$=80.4,
∴此时应录取乙.
点评 本题考查加权平均数,解题的关键是明确题意,找出所求问题需要的条件,会计算加权平均数.


科目:初中数学 来源: 题型:解答题
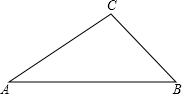 已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,
已知:如图,在△ABC中,∠ABC=45°,tanA=$\frac{3}{4}$,AB=14,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
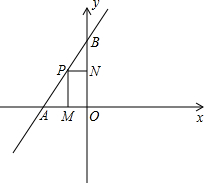 如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.
如图,在平面直角坐标系中,直线y=$\frac{3}{2}$x+6与x轴交于点A,与y轴交于点B,P为线段AB上一动点(不与A,B两点重合),过点P作PM⊥x轴,PN⊥y轴,垂足分别为M,N.设OM=a,四边形PMON面积为s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程 | 收费 |
| 2km以内(含2km) | 10.0 |
| 2km以上,每增加1km | 1.40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,CD与⊙O相切于点C,且OD⊥BC,垂足为F,OD交⊙O于点E.
如图,AB为⊙O的直径,CD与⊙O相切于点C,且OD⊥BC,垂足为F,OD交⊙O于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com