
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D.下列结论中正确的有( )
(1)ED=EC;(2)OD=OC;(3)∠ECD=∠EDC;(4)EO平分∠DEC;(5)OE⊥CD;(6)直线OE是线段CD的垂直平分线.
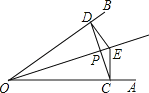
A. 3个B. 4个C. 5个D. 6个
【答案】D
【解析】
根据角平分线上的点到角的两边距离相等可得EC=ED,再利用“HL”证明Rt△OCE和Rt△ODE全等,根据全等三角形对应边相等可得OD=OC,全等三角形对应边相等可∠ECD=∠EDC,再根据等腰三角形三线合一的性质和角平分线的定义解答.
∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴EC=ED,故(1)正确;
在Rt△OCE和Rt△ODE中,![]() ,
,
∴Rt△OCE≌Rt△ODE(HL),
∴OD=OC,∠ECD=∠EDC,故(2)(3)正确;
∴EO平分∠DEC,故(4)正确;
∵OC=OD,OE平分∠AOB,
∴OE⊥CD,故(5)正确;
直线OE是线段CD的垂直平分线,故(6)正确;
综上所述,6个结论都正确.
故选:D.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】《教育导报》记者就四川省农村中小学教师阅读状况进行了一次问卷调查,并根据调查结果绘制了教师每年阅读书籍数量的统计图(不完整).设x表示阅读书籍的数量(x为正整数,单位:本).其中A:1≤x≤3; B:4≤x≤6; C:7≤x≤9;D:x≥10.请你根据两幅图提供的信息解答下列问题:
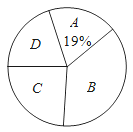
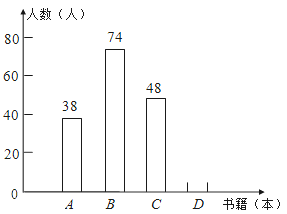
(1)本次共调查了多少名教师?
(2)补全条形统计图;
(3)计算扇形统计图中扇形D的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 内任意一点,
内任意一点,![]() ,点
,点![]() 和点
和点![]() 分别是射线
分别是射线![]() 和射线
和射线![]() 上的动点
上的动点![]() 周长的最小值是
周长的最小值是![]() ,则
,则![]() 的度数是( )
的度数是( )
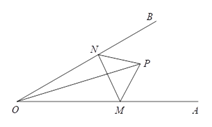
A. 25度 B. 30度 C. 35度 D. 40度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量![]() (单位:升)与时间
(单位:升)与时间![]() (单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,
(单位:分)之间的关系如图所示,则进水速度是______升/分,出水速度是______升/分,![]() 的值为______.
的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平画直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,将直线
,将直线![]() 沿
沿![]() 轴向右平移2个单位长度交
轴向右平移2个单位长度交![]() 轴于
轴于![]() ,交
,交![]() 轴于
轴于![]() ,交直线
,交直线![]() 于
于![]() .
.

(1)直接写出直线![]() 的解析式为______,
的解析式为______,![]() ______.
______.
(2)在直线![]() 上存在点
上存在点![]() ,使
,使![]() 是
是![]() 的中线,求点
的中线,求点![]() 的坐标;
的坐标;
(3)如图2,在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连接BD.

(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,若关于 x 的一元一次方程 ax=b 的解为 x=ba,则称该方程的为差解方程,例如:3x=![]() 的解为x=
的解为x=![]() 且
且![]() =
=![]() -3,则该方程3x=
-3,则该方程3x=![]() 就是差解方程.
就是差解方程.
请根据以上规定解答下列问题
(1)若关于 x 的一元一次方程-5x=m+1 是差解方程,则 m=_____.
(2)若关于 x 的一元一次方程 2x=ab+3a+1 是差解方程,且它的解为 x=a,求代数式(ab+2)2019的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com