
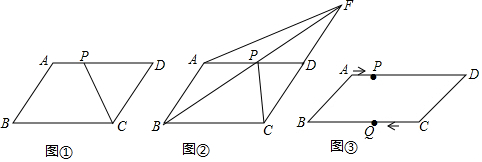
分析 (1)过点P作PQ∥AC,交CD于点Q,由PQ∥l1∥l2结合“两直线平行,内错角相等”找出“∠1=∠CPQ,∠3=∠DPQ”,再通过角的计算即可得出结论;
(2)分别在B点和A点处画方位图,结合(1)的结论即可得到结果;
(3)分两种情况进行讨论:①当点P在A点上方时,过点P作PQ∥AC,交CD于点Q,由PQ∥l1∥l2结合“两直线平行,内错角相等”找出“∠QPC=∠ACP,∠QPD=∠BDP”,再通过角的计算即可得出结论;②当点P在B点下方时,过点P作PQ∥AC,交CD于点Q,利用①的方法可得出结论.
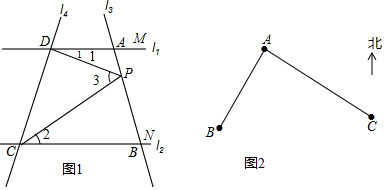
解答 解:(1)当点P在A、B两点间滑动时,∠2=∠1+∠3保持不变.
理由:过点P作PQ∥AC,交CD于点Q,如图1所示.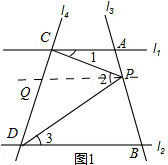
∵PQ∥AC,
∴∠1=∠CPQ,
又∵PQ∥AC,BD∥AC,
∴PQ∥BD,
∴∠3=∠DPQ,
∴∠1+∠3=∠CPQ+∠DPQ,
即∠1+∠3=∠2.
(2)分别在B点和A点处画方位图,如图2所示.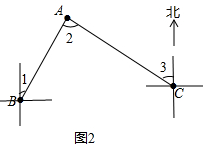
由(1)知:∠2=∠1+∠3
∴∠BAC=32°+56°=88°.
(3)∠CPD=|∠ACP-∠BDP|.
分两种情况:
①当点P在A点上方时,过点P作PQ∥AC,交CD于点Q,如图3所示.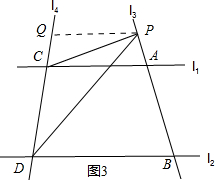
∵PQ∥AC,
∴∠QPC=∠ACP.
又∵PQ∥AC,BD∥AC,
∴PQ∥BD,
∴∠QPD=∠BDP.
又∵∠CPD=∠QPD-∠QPC,
∴∠CPD=∠BDP-∠ACP;
②当点P在B点下方时,过点P作PQ∥AC,交CD于点Q,如图4所示.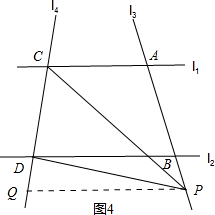
同理可得:∠CPD=∠ACP-∠BDP.
综上所述:∠CPD=|∠ACP-∠BDP|.
点评 本题考查了平行线的性质以及方向角的应用,解题的关键是:(1)根据平行线的性质找出“∠1=∠CPQ,∠3=∠DPQ”;(2)利用(1)中结论进行计算;(3)需要分情况讨论,解决该题型题目时,利用平行线的性质找出相等(或互补)的角是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
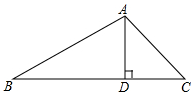 如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )
如图,在△ABC中,sinB=$\frac{1}{2}$,AD⊥BC于点D,∠DAC=45°,AC=10$\sqrt{2}$,则线段BD的长为( )| A. | 10 | B. | 10$\sqrt{2}$ | C. | 10$\sqrt{3}$ | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
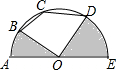 如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )
如图,半圆O的直径AE=8,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为( )| A. | 2π | B. | 4π | C. | 8π | D. | 16π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
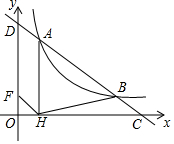 如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.
如图,直线y=-$\frac{1}{2}$x+m交双曲线y=$\frac{k}{x}$(x>0)于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于H,连结BH,若OH:HC=1:5,S△ABH=6,则k的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 价格类型 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 160 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com