
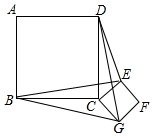
 如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是①②③(填序号)
如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+2b2,其中正确结论是①②③(填序号) 分析 由四边形ABCD与四边形EFGC都为正方形,得到四条边相等,四个角为直角,利用SAS得到三角形BCE与三角形DCG全等,利用全等三角形对应边相等即可得到BE=DG,利用全等三角形对应角相等得到∠1=∠2,利用等角的余角相等及直角的定义得到∠BOD为直角,利用勾股定理求出所求式子的值即可.
解答 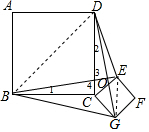 解:设BE,DG交于O,
解:设BE,DG交于O,
∵四边形ABCD和EFGC都为正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCE+∠DCE=∠ECG+∠DCE=90°+∠DCE,即∠BCE=∠DCG,
在△BCE和△DCG中,
$\left\{\begin{array}{l}{BC=DC}\\{∠BCE=∠DCG}\\{CE=CG}\end{array}\right.$,
∴△BCE≌△DCG(SAS),
∴BE=DG,
∴∠1=∠2,
∵∠1+∠4=∠3+∠1=90°,
∴∠2+∠3=90°,
∴∠BOC=90°,
∴BE⊥DG;故①②正确;
连接BD,EG,如图所示,
∴DO2+BO2=BD2=BC2+CD2=2a2,EO2+OG2=EG2=CG2+CE2=2b2,
则BG2+DE2=DO2+BO2+EO2+OG2=2a2+2b2,故③正确.
故答案为:①②③.
点评 此题考查了全等三角形的判定与性质,正方形的性质,勾股定理,熟练掌握性质与定理是解本题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=ax2+2ax+a-1(a>0).
已知二次函数y=ax2+2ax+a-1(a>0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 环数 | 7 | 8 | 9 |
| 人数 | 3 | 4 |
| A. | 3,7 | B. | 3,8 | C. | 4,8 | D. | 1,9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 优惠规则: ①用户手机原有话费不能低于240元; ②办理业务时,首先从手机账户中一次性扣除240元,并把这240元抵为300元话费, ③后将这300元话费分12次,在每月的15号等额返还到手机账户; ④每月1号从手机账户中扣除话费49元,当月不再扣除其他任何费用; 每月1号手机账户的话费余额不足以扣除49元时,视为欠费,则当月不再返还等额话费. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com