
 如图所示,已知等腰梯形ABCD,AD∥BC,若动直线1垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )
如图所示,已知等腰梯形ABCD,AD∥BC,若动直线1垂直于BC,且向右平移,设扫过的阴影部分的面积为S,BP为x,则S关于x的函数图象大致是( )| A. | 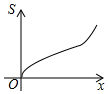 | B. | 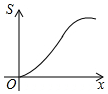 | C. | 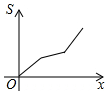 | D. | 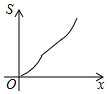 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
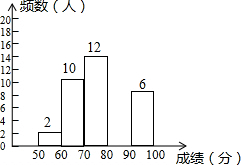 为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且50≤x<100(无满分),将其按分数段分为五组,绘制出以下不完整表格:
为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了“汉子听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉子得1分,本次决赛,学生成绩为x(分),且50≤x<100(无满分),将其按分数段分为五组,绘制出以下不完整表格:| 组别 | 成绩x(分) | 频数(人数) | 频率 |
| 一 | 50≤x<60 | 2 | 0.04 |
| 二 | 60≤x<70 | 10 | 0.2 |
| 三 | 70≤x<80 | 12 | b |
| 四 | 80≤x<90 | a | 0.4 |
| 五 | 90≤x<100 | 6 | 0.12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
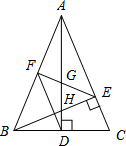 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④∠DFE=2∠DAC;⑤若连接CH,则CH∥EF,其中正确的个数为( )
如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④∠DFE=2∠DAC;⑤若连接CH,则CH∥EF,其中正确的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(±3)^{2}}$=±3 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{{3}^{2}}$=±3 | D. | -$\sqrt{{3}^{2}}$=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com