
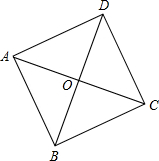
 如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )
如图,在?ABCD中,AC⊥BD于点O,若增加一个条件,使得四边形ABCD是正方形,则下列条件中,不正确的是( )| A. | AC=BD | B. | AB=BC | C. | ∠ABC=90° | D. | AO=BO |
分析 根据菱形的判定定理及正方形的判定定理即可解答.
解答 解:A、∵在?ABCD中,AC⊥BD于O,
∴四边形ABCD是菱形,
当AC=BD时,菱形ABCD就是正方形,故此选项不合题意;
B、∵在?ABCD中,AC⊥BD于O,
∴四边形ABCD是菱形,
当AB=BC,无法得出菱形ABCD是正方形,故此选项符合题意;
C、∵在?ABCD中,AC⊥BD于O,
∴四边形ABCD是菱形,
当∠ABC=90°时,菱形ABCD就是正方形,故此选项不合题意;
D、∵在?ABCD中,AC⊥BD于O,
∴四边形ABCD是菱形,
当AO=BO时,则AO=BO=CO=DO,故菱形ABCD就是正方形,故此选项不合题意;
故选:B.
点评 此题主要考查了正方形的判定,解答此题的关键是熟练掌握正方形的判定定理,即对角线相等的菱形是正方形.


科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
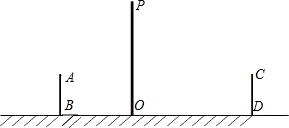 如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.
如图,是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
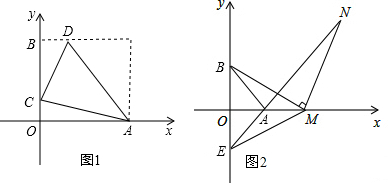
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
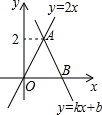 如图,函数y=kx+b(k≠0)的图象经过点B,与函数y=2x的图象交于点A,若△AOB的面积为2,则b等于( )
如图,函数y=kx+b(k≠0)的图象经过点B,与函数y=2x的图象交于点A,若△AOB的面积为2,则b等于( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| (1)(-2)+(-7); | (2)-32-5; | (3)(-30.5)×0.2; |
| (4)12-(-18)+(-7)-15; | (5)(-$\frac{3}{4}$)×(-1$\frac{1}{2}$)×0÷(-2$\frac{1}{4}$); | (6)-9×(-11)÷3÷(-3); |
| (7)-18÷2$\frac{1}{4}$-$\frac{4}{9}$÷(-$\frac{2}{3}$); | (8)($\frac{9}{10}$-$\frac{2}{15}$+$\frac{1}{6}$)×30; | (9)1-3.9÷[1-$\frac{3}{4}$-(-0.5)]. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个等腰直角三角形 | B. | 各有一个角是98°的等腰三角形 | ||
| C. | 与同一个多边形相似的两个多边形 | D. | 有一个角是80°的两个等腰三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com