
科目:初中数学 来源: 题型:填空题
 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点;然后从4→3为第二次“移位”.若小宇从编号为3的顶点开始,第2017次“移位”后,则他所处顶点的编号是1.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为2的顶点上时,那么他应走2个边长,即从2→3→4为第一次“移位”,这时他到达编号为4的顶点;然后从4→3为第二次“移位”.若小宇从编号为3的顶点开始,第2017次“移位”后,则他所处顶点的编号是1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{{3}^{5}}{5×{2}^{9}}$ | B. | $\frac{5×{3}^{5}}{{2}^{12}}$ | C. | $\frac{5×{3}^{6}}{{2}^{14}}$ | D. | $\frac{{3}^{7}}{5×{2}^{11}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
如图,一边靠校园围墙,其他三边用总长为80米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )| A. | 40米 | B. | 30米 | C. | 20米 | D. | 10米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
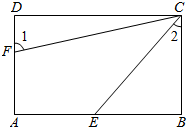 如图,已知四边形ABCD是平行四边形,并且∠A=∠D.
如图,已知四边形ABCD是平行四边形,并且∠A=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 盈亏情况 | 128.3 | -25.6 | -15 | 27 | -7 | 36.5 | 98 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com