
分析 (1)根据画角的方法作∠E等于已知角∠CBA;
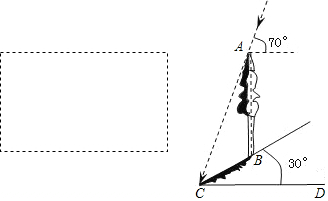
(2)本题可通过构造直角三角形来解答,延长AB交CD于点E,则AE⊥CD,E为垂足,直角三角形BCE中,已知BC的长,∠BCD的度数,那么可求出CE和BE的长,直角三角形ACF中,已知∠CAE=180-90-70=20°,前面又得到了CE,BE的长,那么就可求出AE的长,AB=AE-BE就能求出AB的长了.
解答  解:(1)如图所示:∠E即为所求;
解:(1)如图所示:∠E即为所求;
(2)延长AB交CD于点E,则AE⊥CD,E为垂足.
由题意得:∠BCE=30°,∠ACE=70°,BC=4米.
在Rt△BCE中,BE=$\frac{1}{2}$BC=2(米),
CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=2$\sqrt{3}$(米),
在Rt△ACE中,tan∠ACE=$\frac{AE}{CE}$,
即tan70°=AE:CE,
∴AB=2$\sqrt{3}$tan70°-2≈2×1.73×2.75-2≈9.5-2=7.5(米).
答:树高AB约为7.5米.
点评 考查了作图-应用与设计作图,解直角三角形的应用-坡度坡角问题,本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
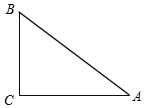 在Rt△ABC中,∠C=90°,AC=4,BC=3,
在Rt△ABC中,∠C=90°,AC=4,BC=3,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com