
【题目】小明从A地向南偏东m°(0<m<90)的方向行走到B地,然后向左转30°行走到C地,则下面表述中,正确的个数是( )
①B可能在C的北偏西m°方向;
②当m<60时,B在C的北偏西(m+30)°方向;
③B不可能在C的南偏西m°方向;
④当m>60时,B在C的南偏西(150-m)°方向
A. 1B. 2C. 3D. 4
【答案】B
【解析】
分三种情况讨论:①当0°<m<60°时;②当m=60°时;③当60°<m<90°时;分别画出图形,根据方位角的知识即可解决问题.
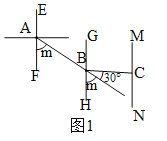
分三种情况讨论:①当0°<m<60°时,如图1.
∵0°<m<60°,∴30°<m+30°<90°,∴∠MCB= (m+30)°,∴B在C的北偏西(m+30)°方向,故②正确;
∵m+30>m,∴B不可能在C的北偏西m°方向;∴①错误;
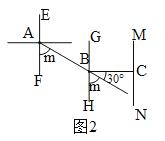
②当m=60°时,如图2,m+30°=90°,∴∠MCB= 90°,∴B在C的正西方向;
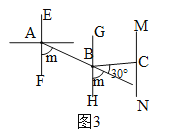
③当60°<m<90°时,如图3.
∵60°<m<90°,∴90°<m+30°<120°,∴∠BCN= 180°-(m+30°)=(150-m)°,∴B在C的南偏西(150-m)°方向,故④正确.
当150-m= m时,解得:m=75°,∴当m=75°时,B在C的南偏西m°方向,故③错误.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3 . 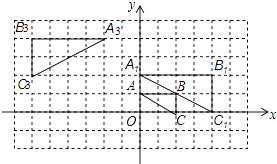
(1)△ABC与△A1B1C1的位似比等于;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经知道,有一个内角是直角的三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边.数学家已发现在一个直角三角形中,两条直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么可以用数学语言表达为:
,那么可以用数学语言表达为:![]() .
.
(1)在图中,若![]() ,
,![]() ,则
,则![]() 等于多少;
等于多少;
(2)观察图,利用面积与代数恒等式的关系,试说明![]() 的正确性.其中两个相同的直角三角形边
的正确性.其中两个相同的直角三角形边![]() 、
、![]() 在一条直线上;
在一条直线上;
(3)如图③所示,折叠长方形![]() 的一边
的一边![]() ,使点
,使点![]() 落在
落在![]() 边的点
边的点![]() 处,已知
处,已知![]() ,
,![]() ,利用上面的结论求的长.
,利用上面的结论求的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=5,BC=3,AC=4,点E,F分别是AB,BC的中点.以下结论错误的是( )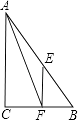
A.△ABC是直角三角形
B.AF是△ABC的中位线
C.EF是△ABC的中位线
D.△BEF的周长为6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线l1:y=﹣x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,﹣2).
(1)求抛物线l2的解析式;
(2)点P为线段AB上一动点(不与A、B重合),过点P作y轴的平行线交抛物线l1于点M,交抛物线l2于点N.
①当四边形AMBN的面积最大时,求点P的坐标;
②当CM=DN≠0时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com