
 ��ͼ����֪������y=$\frac{1}{3}$x2+bx+c������ABC���������㣬���е�A��0��1������B��9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮
��ͼ����֪������y=$\frac{1}{3}$x2+bx+c������ABC���������㣬���е�A��0��1������B��9��10����AC��x�ᣬ��P��ֱ��AC�·��������ϵĶ��㣮���� ��1�����ݴ���ϵ�������ɵú�������ʽ��
��2������ƽ����x���ֱ���ϵ����������ȣ��ɵ�C��������꣬�����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�C�����꣬���ݴ���ϵ�������ɵ�AB�Ľ���ʽ������ֱ���ϵĵ����㺯������ʽ���ɵ�E�����꣬����ƽ����y���ֱ���������ľ����ǽϴ�����������С�������꣬�ɵ�PE�ij�����������ĺͲ�ɵö��κ��������ݶ��κ��������ʣ��ɵô𰸣�
��3�����ݵ���ֱ�������ε����ʣ��ɵá�PCF=��EAF���������������ε��ж����ɵù���t�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��� �⣺��1����A��0��1����B��9��10�����뺯������ʽ����
$\left\{\begin{array}{l}{\frac{1}{3}��81+9b+c=10}\\{c=1}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-2}\\{c=1}\end{array}\right.$��
�����ߵĽ���ʽy=$\frac{1}{3}$x2-2x+1��
��2����AC��x�ᣬA��0��1����
��$\frac{1}{3}$x2-2x+1=1�����x1=6��x2=0���ᣩ����C������Ϊ��6��1����
�ߵ�A��0��1������B��9��10����
��ֱ��AB�Ľ���ʽΪy=x+1����P��m��$\frac{1}{3}$m2-2m+1��
��E��m��m+1����
��PE=m+1-��$\frac{1}{3}$m2-2m+1��=-$\frac{1}{3}$m2+3m��
��AC��PE��AC=6��
��S�ı���AECP=S��AEC+S��APC=$\frac{1}{2}$AC•EF+$\frac{1}{2}$AC•PF
=$\frac{1}{2}$AC•��EF+PF��=$\frac{1}{2}$AC•EP=$\frac{1}{2}$��6��-$\frac{1}{3}$m2+3m��=-m2+9m=-��m-$\frac{9}{2}$��2+$\frac{81}{4}$��
��0��m��6��
�൱m=$\frac{9}{2}$ʱ���ı���AECP��������ֵ��$\frac{81}{4}$����ʱP��$\frac{9}{2}$��-$\frac{5}{4}$����
��3����y=$\frac{1}{3}$x2-2x+1=$\frac{1}{3}$��x-3��2-2��
P��3��-2����PF=yF-yp=3��CF=xF-xC=3��
��PF=CF��
���PCF=45�㣬
ͬ���ɵá�EAF=45�㣬
���PCF=��EAF��
����ֱ��AC�ϴ������������õ�Q����Q��t��1����AB=9$\sqrt{2}$��AC=6��CP=3$\sqrt{2}$��
����C��P��QΪ��������������ABC���ƣ�
�ٵ���CPQ�ס�ABCʱ��$\frac{CQ}{AC}$=$\frac{CP}{AB}$��$\frac{6-t}{6}$=$\frac{3\sqrt{2}}{9\sqrt{2}}$��
���t=4��
Q��4��1����
�ڵ���CQP�ס�ABCʱ����$\frac{CQ}{AB}$=$\frac{CP}{AC}$��
$\frac{6-t}{9\sqrt{2}}$=$\frac{3\sqrt{2}}{6}$��
���t=-3��
Q��-3��1����
��������������PΪ�����ߵĶ���ʱ����ֱ��AC�ϴ��ڵ�Q��ʹ����C��P��QΪ��������������ABC���ƣ�Q�������Ϊ��4��1����-3��1����
���� ���⿼���˶��κ����ۺ��⣬�⣨1���Ĺؼ��Ǵ���ϵ�������⣨2���Ĺؼ�����������ĺͲ�ó����κ������������˶��κ��������ʣ�ƽ�����������ֱ���������ľ����ǽϴ���������С�����ꣻ�⣨3���Ĺؼ����������������ε����ʵij�����CQ�ı�����Ҫ�������ۣ��Է���©��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | 2 | C�� | -1 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
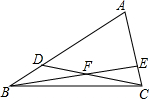 �ڡ�ABC�У���D��E�ֱ���AB��AC�ϣ���CD��BE�ཻ�ڵ�F����֪��BDF�����Ϊ12����BCF�����Ϊ16����CEF�����Ϊ12�����ı���ADFE�����Ϊ72��
�ڡ�ABC�У���D��E�ֱ���AB��AC�ϣ���CD��BE�ཻ�ڵ�F����֪��BDF�����Ϊ12����BCF�����Ϊ16����CEF�����Ϊ12�����ı���ADFE�����Ϊ72���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{m-a}{b}$���� | B�� | $\frac{m}{a+b}$���� | C�� | $\frac{m-a+b}{b}$���� | D�� | $\frac{m-a-b}{b}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
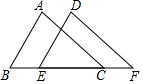 ��ͼ����B��E��C��F��ͬһ��ֱ���ϣ�AC��DF��AC=DF��BE=CF��
��ͼ����B��E��C��F��ͬһ��ֱ���ϣ�AC��DF��AC=DF��BE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��5��1�� | B�� | ��-1��5�� | C�� | ��-3��-$\frac{5}{3}$�� | D�� | ��$\frac{5}{3}$��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ֱ��m��n����ƽ��ֱ������ϵxOy�У�x���m��y���n�������O1Ϊԭ�㣬��A ������Ϊ��1��1��������O1ƽ��2$\sqrt{2}$����λ���ȵ���O2����A��λ�ò��䣬�����O2Ϊԭ�㣬��ô��A����������ǣ�������
��ͼ��ֱ��m��n����ƽ��ֱ������ϵxOy�У�x���m��y���n�������O1Ϊԭ�㣬��A ������Ϊ��1��1��������O1ƽ��2$\sqrt{2}$����λ���ȵ���O2����A��λ�ò��䣬�����O2Ϊԭ�㣬��ô��A����������ǣ�������| A�� | ��3��-1�� | B�� | ��1��-3�� | C�� | ��-2��-1�� | D�� | ��2$\sqrt{2}$+1��2$\sqrt{2}$+1�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com