
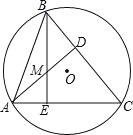
【题目】如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
A.2![]() B.2
B.2![]() C.4
C.4![]() D.6
D.6
【答案】A
【解析】
试题分析:作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,推出∠HCA=∠HBA=90°,证出四边形HBMC为平行四边形,求出HC,根据垂径定理求出AF,根据中位线得出OF,再根据勾股定理求出OA即可. 作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,如图所示: ∵AH为直径, ∴∠HCA=∠HBA=90°, ∵CN⊥AB,BE⊥AC,
∴∠CNA=∠BEA=90° ∴∠HBA=∠CNA,∠HCA=∠BEA, ∴HB∥CN,HC∥BE, ∴四边形HBMC为平行四边形, ∴BM=HC=4, ∵OF⊥CC,OF过O, ∴根据垂径定理:CF=FA=![]() AC=4, ∵AO=OH, ∴OF为△ACH的中位线, ∴OF=
AC=4, ∵AO=OH, ∴OF为△ACH的中位线, ∴OF=![]() HC=2, ∴在Rt△AOF中,OA2=OF2+AF2=22+42=20, ∴AC=2
HC=2, ∴在Rt△AOF中,OA2=OF2+AF2=22+42=20, ∴AC=2![]() ;
;



科目:初中数学 来源: 题型:
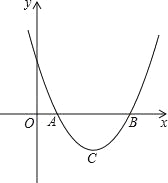
【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( ) 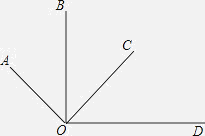
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
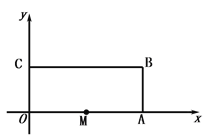
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(8,0),C点的坐标为(0,4),点B在第一象限内,点M从原点出发,以每秒2个单位长度的速度沿着O-A-B-C-O的路线移动(运动后到O点停止运动).
(1)当点M移动了5秒时,点M的坐标是 ;
(2)在移动过程中,点M到y轴的距离为6个单位长度时,则点M移动的时间是 ;
(3)在移动过程中,若MB=MO,求点M移动的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com