

分析 (1)①连接AC,证明△BAE≌△CAF,得到y与x之间的函数关系式;
②根据△BAE≌△CAF,得到四边形AECF面积=△ABC的面积,得到答案;
③根据△CEF的面积最大时,△AEF的面积最小,求出△CEF的面积最大时x的值即可;
(2)连接AC,证明△CAE≌△DAF即可.
解答 解:(1)①如图1,连接AC,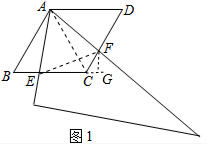
∵四边形ABCD是菱形,∠B=60°,
∴△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵∠EAF=60°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{AB=AC}\\{∠B=∠ACF}\end{array}\right.$,
∴△BAE≌△CAF,
∴CF=BE,
∴y=10-x;
②∵△BAE≌△CAF,
∴四边形AECF面积=△AEC的面积+△ACF的面积=△AEC的面积+△ABE的面积=△ABC的面积,
∴四边形AECF面积保持不变;
③存在.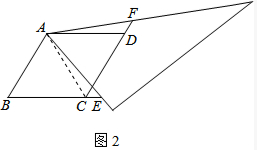
∵四边形AECF面积保持不变,
∴△CEF的面积最大时,△AEF的面积最小,
作FG⊥BC交BC的延长线于G,
△CEF的面积=$\frac{1}{2}$×EC×FG=$\frac{1}{2}$×(10-x)×x×sin60°=-$\frac{\sqrt{3}}{4}$x2+$\frac{5\sqrt{3}}{2}$x,
当x=5时,△CEF的面积最大,△AEF的面积最小,
∴点E为BC的中点,
∴∠BAE=30°;
(2)如图2,连接AC,
由(1)①得,△CAE≌△DAF,
∴CE=DF,
∴y=x-10.
点评 本题考查的是菱形的性质、二次函数的性质、锐角三角函数的定义,掌握菱形的四条边相等、一组对角线平分一组对角是解题的关键,注意二次函数的性质的灵活运用.


科目:初中数学 来源: 题型:解答题
 2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛,在全州安全知识竞赛结束后,通过网上查询,某校一名班主任对本班成绩(成绩取整数,满分100分)作了统计分析,绘制成如下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
2016年黔西南州教育局组织全州中小学生参加全省安全知识网络竞赛,在全州安全知识竞赛结束后,通过网上查询,某校一名班主任对本班成绩(成绩取整数,满分100分)作了统计分析,绘制成如下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:| 分组(分) | 频数 | 频率 |
| 50<x 60 | 2 | 0.04 |
| 60<x 70 | 12 | a |
| 70<x<80 | b | 0.36 |
| 80<x 90 | 14 | 0.28 |
| 90<x 100 | c | 0.08 |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=74°,则∠NPB′=16°.
如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=74°,则∠NPB′=16°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com