
【题目】已知,如图,![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,![]() 于点
于点![]() 取
取![]() 的中点
的中点![]() 连接
连接![]() 并延长交
并延长交![]() 于
于![]() .连接
.连接![]() .
.

![]() ①直接写出:
①直接写出:![]() 与
与![]() 的位置关系是________,
的位置关系是________,![]() 与
与![]() 的数量关系是 ;
的数量关系是 ;
②请任意选择上述关系中的一个加以证明.
![]() 已知,
已知,![]() ,
,![]() 若
若![]() 与
与![]() 交于点
交于点![]() 求
求![]() 的长.
的长.
【答案】(1)①![]() ;②见解析;(2)
;②见解析;(2)![]() .
.
【解析】
(1)①根据![]() 和
和![]() 是等腰直角三角形,得到∠ABC=∠ACB=45°,根据
是等腰直角三角形,得到∠ABC=∠ACB=45°,根据![]() ,得到∠ECB=∠CED=90°,推出ED∥BC,证得∠EDN=∠MBN,从而证明△BMN≌△DEN,得到BM=EC,再证明△ABM≌△ACE,推出△MAE是等腰直角三角形,得到
,得到∠ECB=∠CED=90°,推出ED∥BC,证得∠EDN=∠MBN,从而证明△BMN≌△DEN,得到BM=EC,再证明△ABM≌△ACE,推出△MAE是等腰直角三角形,得到![]() ;
;
②如①的证明过程;
![]() 过点
过点![]() 作
作![]() 于点
于点![]() 得到四边形
得到四边形![]() 是正方形,由勾股定理求出
是正方形,由勾股定理求出![]() ,
,![]() ,得到
,得到![]() ,由勾股定理求出
,由勾股定理求出![]() ,根据
,根据![]() 证得△DEF∽△BCF,求出DF的长度.
证得△DEF∽△BCF,求出DF的长度.
(1)①∵![]() 和
和![]() 是等腰直角三角形,
是等腰直角三角形,
∴AB=AC,EC=ED,∠BAC=∠CED=90°,
∴∠ABC=∠ACB=45°,
∵![]() ,
,
∴∠ECB=∠CED=90°,
∴ED∥BC,
∴∠EDN=∠MBN,
∵N是BD的中点,
∴BN=DN,
∵∠BNM=∠END,
∴△BMN≌△DEN,
∴BM=DE,MN=EN,
∴BM=EC,
∵∠ECB=90°,∠ACB=45°,
∴∠ACE=∠ABC=45°,
∵AB=AC,
∴△ABM≌△ACE,
∴AM=AE,∠BAM=∠CAE,
∵∠BAM+∠CAM=90°,
∴∠MAE=∠CAE+∠CAM=90°,
∴△MAE是等腰直角三角形,
∵MN=NE,
∴![]() ,
,
故答案为:![]() ;
;
![]() 选
选![]() 给予证明:
给予证明:
![]() ,
,
![]()
![]()
![]() 点
点![]() 是
是![]() 的中点,
的中点,
![]()
在![]() 和
和![]() 中,
中,
![]() ,
,![]()
![]() ,
,
![]() ;
;
∵△ABC和![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]() ,
,
![]() ;
;
![]() ,
,
![]()
![]()
在![]() 和
和![]() 中,
中,
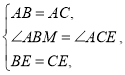
![]()
![]() ,
,![]() ,
,
![]()
即![]() ;
;
又![]() .
.
![]() ,
,
(说明:由![]() 可得
可得![]() );
);
![]() 过点
过点![]() 作
作![]() 于点
于点![]()
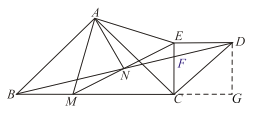
则四边形![]() 是正方形,
是正方形,
![]()
![]() ,
,
在等腰直角![]() 中,
中,
![]()
![]()
![]() ,
,
在直角![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
由![]() 得
得![]()
![]() ,
,
![]() ,
,
![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】(4分)一元二次方程![]() 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
【答案】A.
【解析】
试题∵△=![]() ,∴方程有两个不相等的实数根.故选A.
,∴方程有两个不相等的实数根.故选A.
考点:根的判别式.
【题型】单选题
【结束】
9
【题目】已知直线y=kx(k>0)与双曲线![]() 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
A.﹣6 B.﹣9 C.0 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
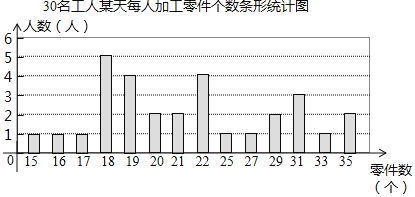
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某酒店试销售某种套餐,试销一段时间后发现,每份套餐的成本为7元,该店每天固定支出费用为200元(不含套餐成本). 若每份售价不超过10元,每天可销售300份;若每份售价超过10元,每提高1元,每天的销售量就减少30份. 设该店每份套餐的售价为x(x≥7)元,每天的销售量为y份,每天的利润为M元.
(1)直接写出y与x的函数关系式;
(2)求出M与x的函数关系式;
(3)若该店既要吸引顾客,使每天的销售量较大,又要获取最大的利润,则每份套餐的售价应定为多少元(为了便于计算,每份套餐的售价取整数)?此时,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() .
.
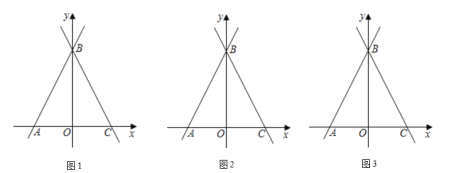
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]()
![]() ,求
,求![]() 与
与![]() 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 时,求直线
时,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动,购买了一批图书.已知购买科普类图书花费了10000元,购买文学类图书花费了9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普类图书的数量比购买文学类图书数量少100本,科普类图书平均每本的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月12日是我国义务植树节.某校组织九年级学生开展义务植树活动,在活动结束后随机调查了30名学生每人植树的棵数,根据调查获取的样本数据,制作了条形统计图和扇形统计图.请根据相关信息,解答下列问题:
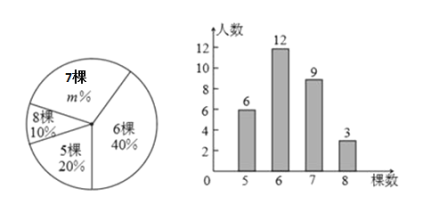
(1)扇形图中![]() 的值是 ;
的值是 ;
(2)求这30个样本数据的平均数、众数、中位数;
(3)若本次活动九年级共有300名学生参加,估计本次活动共植树约为多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校5位家长志愿者(3男2女)为倡导“学习雷锋、奉献他人、提升白己”的志愿服务理念,积极参与文明城市创建活动,在人、车流动量较大的重要路口、路段开展“文明劝导”志愿服务活动.
(1)若随机安排一人到西华北路路段,则恰是男志愿者的概率为______;
(2)若随机安排两人到莲乡大道路段,用列表法求出“全是男志愿者”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com