
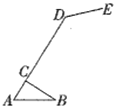
【题目】如图是一种简易台灯的结构图,灯座为△ABC,A、C、D在同一直线上,量得∠ACB=90°,∠A=60°,AB=16cm,∠ADE=135°,灯杆CD长为40cm,灯管DE长为15cm.求台灯的高(即台灯最高点E到底盘AB的距离).(结果取整,参考数据sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,![]() ≈1.73)
≈1.73)
【答案】台灯的高约为45cm.
【解析】
如图,作DG⊥AB,EF⊥AB,交AB延长线于G、F,DH⊥EF于H,可得四边形DGFH是矩形,可得DG=FH,根据∠A的余弦可求出AC的长,进而可得AD的长,根据∠A的正弦即可求出DG的长,由∠ADE=135°可得∠EDH=15°,根据∠DEH的正弦可得EH的长,根据EF=EH+FH求出EF的长即可得答案.
如图,作DG⊥AB,EF⊥AB,交AB延长线于G、F,DH⊥EF于H,
∴四边形DGFH是矩形,
∴DG=FH,
∵∠A=60°,AB=16,
∴AC=AB·cos60°=16×![]() =8,
=8,
∴AD=AC+CD=8+40=48,
∴DG=AD·sin60°=24![]() ,
,
∵DH⊥EF,AF⊥EF,
∴DH//AF,
∴∠ADH=180°-∠A=120°,
∵∠ADE=135°,
∴∠EDH=∠ADE-∠ADH=15°,
∵DE=15,
∴EH=DE·sin15°≈3.9,
∴EF=EH+FH=EH+DG=24![]() +3.9≈45,
+3.9≈45,

答:台灯的高约为45cm.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】在某一个学校的运动俱乐部里面有三大筐数量相同的球,甲每次从第一个大筐中取出9个球;乙每次从第二个大筐中取出7个球;丙则是每次从第三个大筐中取出5个球.到后来甲、乙、丙三人都记不清各自取过多少次球了,于是管理人员查看发现第一个大筐中还剩下7个球,第二个大筐还剩下4个球,第三个大筐还剩下2个球,那么根据上述情况可以推知甲至少取了______次.
查看答案和解析>>
科目:初中数学 来源: 题型:
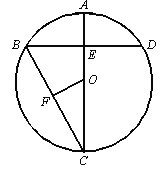
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半径;
(2)求O到弦BC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学一幢教学楼的顶部竖有一块写有“校训”的宣传牌![]() ,
,![]() 米,王老师用测倾器在
米,王老师用测倾器在![]() 点测得
点测得![]() 点的仰角为
点的仰角为![]() ,再向教学楼前进9米到达
,再向教学楼前进9米到达![]() 点,测得点
点,测得点![]() 的仰角为
的仰角为![]() ,若测倾器的高度
,若测倾器的高度![]()
![]()
![]() 米,不考虑其它因素,求教学楼
米,不考虑其它因素,求教学楼![]() 的高度.(结果保留根号)
的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
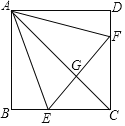
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE=![]() S△CEF.其中正确的是( )
S△CEF.其中正确的是( )
A. ①③B. ②④C. ①③④D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() .抛物线的解析式为
.抛物线的解析式为![]() .
.


(1)如图一,若抛物线经过![]() ,
,![]() 两点,直接写出
两点,直接写出![]() 点的坐标 ;抛物线的对称轴为直线 ;
点的坐标 ;抛物线的对称轴为直线 ;
(2)如图二:若抛物线经过![]() 、
、![]() 两点,
两点,
①求抛物线的表达式.
②若点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() 交抛物线于点
交抛物线于点![]() .当线段
.当线段![]() 最长时,求点
最长时,求点![]() 的坐标;
的坐标;
(3)若![]() ,且抛物线与矩形
,且抛物线与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
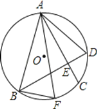
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究反比例函数![]() 的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量x的取值范围是全体非零实数,因此函数图象会被y轴分成两部分;其次,分析解析式,得到y随x的变化趋势:当x>0时,随着x值的增大,y的值减小,且逐渐接近于零,随着x值的减小,y的值会越来越大,由此,可以大致画出
的图象与性质时,我们对函数解析式进行了深入分析.首先,确定自变量x的取值范围是全体非零实数,因此函数图象会被y轴分成两部分;其次,分析解析式,得到y随x的变化趋势:当x>0时,随着x值的增大,y的值减小,且逐渐接近于零,随着x值的减小,y的值会越来越大,由此,可以大致画出![]() 在x>0时的部分图象,如图1所示.利用同样的方法,我们可以研究函数
在x>0时的部分图象,如图1所示.利用同样的方法,我们可以研究函数![]() 的图象与性质.
的图象与性质.

(1)该函数自变量x的取值范围_______________;
(2)通过分析解析式画出部分函数图象,如图2所示.请沿此思路在图2中完善函数图象的草图并标出此函数图象与y轴的交点A;(画出网格区域内的部分即可)
(3)观察图象,写出该函数的一条性质: ;
(4)若关于x的方程![]() 有两个不相等的实数根,结合图象,直接写出实数a的取值范围: .
有两个不相等的实数根,结合图象,直接写出实数a的取值范围: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com