
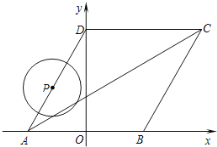
【题目】如图所示,菱形ABCD的顶点A、B在![]() 轴上,点A在点B的左侧,点D在
轴上,点A在点B的左侧,点D在![]() 轴的正半轴上,
轴的正半轴上,![]() ,点A的坐标为
,点A的坐标为![]() .
.
(1)求D点的坐标.
(2)求直线AC的函数关系式.
(3)动点P从点A出发,以每秒1个单位长度的速度,按照![]() 的顺序在菱形的边上匀速运动一周,设运动时间为
的顺序在菱形的边上匀速运动一周,设运动时间为![]() 秒.求
秒.求![]() 为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
为何值时,以点P为圆心、以1为半径的圆与对角线AC相切?
【答案】(1)(0,2![]() );(2)
);(2)![]() ;(3)t=2或6或10或14
;(3)t=2或6或10或14
【解析】
(1)在Rt△AOD中,根据OA的长以及∠BAD的正切值,即可求得OD的长,从而得到D点的坐标;
(2)根据点A、C的坐标,利用待定系数法可求得直线AD的解析式.
(3)由于点P沿菱形的四边匀速运动一周,那么本题要分作四种情况考虑:
在Rt△OAD中,易求得AD的长,也就得到了菱形的边长,而菱形的对角线平分一组对角,那么∠DAC=∠BAC=∠BCA=∠DCA=30°;
①当点P在线段AD上时,若⊙P与AC相切,由于∠PAC=30°,那么AP=2R(R为⊙P的半径),由此可求得AP的长,即可得到t的值;
②③④的解题思路与①完全相同,只不过在求t值时,方法略有不同.
解:(1)∵点A的坐标为(-2,0),∠BAD=60°,∠AOD=90°,
∴OD=OAtan60°=2![]() ,AD=4,
,AD=4,
∴点D的坐标为(0,2![]() );
);
(2)根据(1)知点D的坐标为(0,2![]() )
)
∵AD=CD,CD∥AB,
∴C(4,2![]() );
);
设直线AC的函数表达式为y=kx+b(k≠0),
∵A(-2,0),C(4,2![]() ),
),
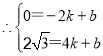
解得: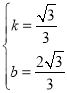
∴直线AC的解析式为![]() ;
;
(3)∵四边形ABCD是菱形,
∴∠DCB=∠BAD=60°,
∴∠1=∠2=∠3=∠4=30°,
AD=DC=CB=BA=4,
如图所示:
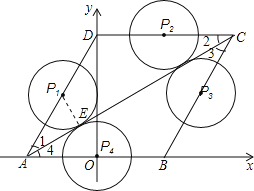
①点P在AD上与AC相切时,
连接P1E,则P1E⊥AC,P1E=r,
∵∠1=30°,
∴AP1=2r=2,
∴t1=2.
②点P在DC上与AC相切时,
CP2=2r=2,
∴AD+DP2=6,
∴t2=6.
③点P在BC上与AC相切时,
CP3=2r=2,
∴AD+DC+CP3=10,
∴t3=10.
④点P在AB上与AC相切时,
AP4=2r=2,
∴AD+DC+CB+BP4=14,
∴t4=14,
∴当t=2或6或10或14时,以点P为圆心、以1为半径的圆与对角线AC相切.
故答案为:(1)(0,2![]() );(2)
);(2)![]() ;(3)t=2或6或10或14.
;(3)t=2或6或10或14.


科目:初中数学 来源: 题型:
【题目】某公司开发处一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.

(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为W(元),求W与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第几天的日销售利润最大,最大日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() .且
.且![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 时,求⊙
时,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
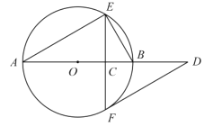
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,请补全图形;若
,请补全图形;若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
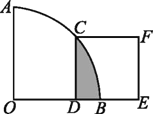
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,阴影部分的面积为________
时,阴影部分的面积为________
查看答案和解析>>
科目:初中数学 来源: 题型:
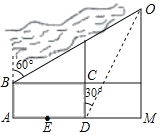
【题目】如图所示,小亮家在点O处,其所在学校的校园为矩形ABCD,东西长AD=1000米,南北长AB=600米.学校的南正门在AD的中点E处,B为学校的西北角门.小亮从家到学校可以走马路,路线O→M→E(∠M=90°);也可以走沿河观光路,路线O→B.小亮在D处测得O位于北偏东30°,在B处测得O位于北偏东60°小亮从家到学校的两条路线中,长路线比短路线多_____米.(结果保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com