
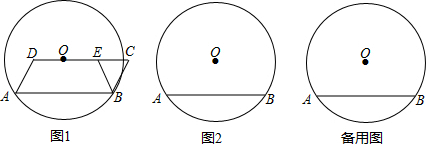
分析 (1)如图1,连接OA,OB,根据等腰三角形的性质得到∠OAB=∠OBA,根据平行四边形的性质得到AD=BC,AB∥CD,∠DAB=∠C,根据全等三角形的性质即可得到结论;
(2)如图2,过O作OH⊥AB于H,由垂径定理得到AH=$\frac{1}{2}$AB=4,连接OA,根据勾股定理得到OH=$\sqrt{O{A}^{2}-A{H}^{2}}$=3,过D作DG⊥AB于G,根据矩形的性质得到DG=OH=3,GH=x,根据勾股定理即可得到结论;
(3)如图3,过D作DG⊥AB于G,CH⊥AB于H,根据全等三角形的性质得到BH=AE,由(2)知,OD=x,BC=y,AG=4-x,DG=CH=3,根据相似三角形的性质即可得到结论.
解答 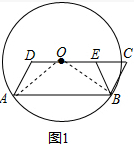 解:(1)如图1,连接OA,OB,
解:(1)如图1,连接OA,OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,∠DAB=∠C,
∴∠CEB=∠ABE,
∵BC=BE,
∴AD=BE,
∴∠C=∠BEC,
∴∠DAB=∠ABE,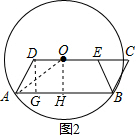
∴∠DAO=∠EBO,
在△ADO与△BEO中,$\left\{\begin{array}{l}{AD=BE}\\{∠DAO=∠EBO}\\{AO=BO}\end{array}\right.$,
∴∠ADO≌△BEO,
∴OD=OE;
(2)如图2,过O作OH⊥AB于H,
∴AH=$\frac{1}{2}$AB=4,
连接OA,
∵OA=5,
∴OH=$\sqrt{O{A}^{2}-A{H}^{2}}$=3,
过D作DG⊥AB于G,
∴四边形DGHO是矩形,
∴DG=OH=3,GH=x,
∴AG=4-x,
∵AD=BC=y,
∴y2=32+(4-x)2,
∴y=$\sqrt{{x}^{2}-8x+25}$(0<x<4);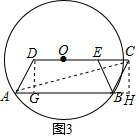
(3)如图3,过D作DG⊥AB于G,CH⊥AB于H,
在Rt△ADG与Rt△BCH中,$\left\{\begin{array}{l}{AD=BC}\\{DG=CH}\end{array}\right.$,
∴Rt△ADG≌Rt△BCH,
∴BH=AE,
由(2)知,OD=x,BC=y,AG=4-x,DG=CH=3,
∴BH=4-x,
∴AH=8+4-x=12-x,
∵CD∥AB,
∴CH⊥CD,AC⊥BE,
∴∠ECA+∠HCB=∠ECA+∠CEB=90°,
∴∠BEC=∠ACH,
∴∠DAG=∠ACH,
∴△ADG∽△ACH,
∴$\frac{AG}{CH}=\frac{DG}{AH}$,即$\frac{4-x}{3}$=$\frac{3}{12-x}$,
∴x=3,x=13(不合题意,舍去),
∴DO=3.
点评 本题考查了垂径定理,全等三角形的判定和性质,相似三角形的判定和性质,平行四边形的性质,矩形的判定和性质,正确的作出辅助线是解题的关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:填空题
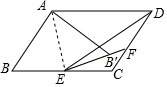 如图,?ABCD中,E为BC上一点,将?ABCD沿AE折叠,点B落在点B′处,EB′的延长线交CD于F,EF=DF,若∠B=60°,∠BAE=40°,则∠CDE的度数为20°.
如图,?ABCD中,E为BC上一点,将?ABCD沿AE折叠,点B落在点B′处,EB′的延长线交CD于F,EF=DF,若∠B=60°,∠BAE=40°,则∠CDE的度数为20°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
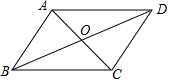 要做一个平行四边形框架,只要将两根木条AC、BD的中点重叠并用钉子固定,这样四边形ABCD就是平行四边形,这种做法的依据是两条对角线分别平分的四边形是平行四边形.
要做一个平行四边形框架,只要将两根木条AC、BD的中点重叠并用钉子固定,这样四边形ABCD就是平行四边形,这种做法的依据是两条对角线分别平分的四边形是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
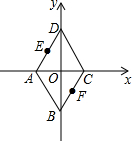 以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,AD的中点E的坐标为(-1,2),则BC的中点F的坐标为(1,-2).
以菱形ABCD的对角线交点O为原点,对角线AC、BD所在直线为坐标轴,建立如图所示直角坐标系,AD的中点E的坐标为(-1,2),则BC的中点F的坐标为(1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
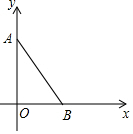 如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.
如图,平面直角坐标系xOy中,已知点A(0,3),点B($\sqrt{3}$,0),连接AB,若对于平面内一点C,当△ABC是以AB为腰的等腰三角形时,称点C是线段AB的“等长点”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
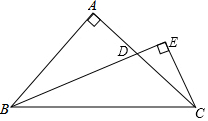 已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )
已知等腰直角三角形ABC,BC是斜边,∠B的平分线交AC于D,过C作CE与BD垂直且交BD延长线于E.已知CE=4,则BD的长为( )| A. | 5 | B. | 8 | C. | $\sqrt{73}$ | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com