
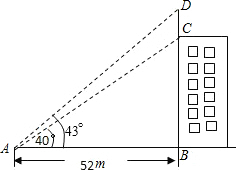
 如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84)
如图,∠BAD=43°,∠BAC=40°,AB=52m,求得避雷针CD的长约4.86m.(结果精确到0.1m)(可用下列参考数据求:sin43°≈0.68,sin40°≈0.64,cos43°≈0.73,cos40°≈0.76,tan43°≈0.93,tan40°≈0.84) 科目:初中数学 来源: 题型:选择题
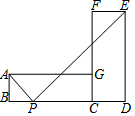 如图,将矩形ABCG(AB<BC)绕点C顺时针旋转90°后得到矩形CFED,点P是线段BD上的一个动点,连接AP、PE,则使∠APE为直角的点P的个数是( )
如图,将矩形ABCG(AB<BC)绕点C顺时针旋转90°后得到矩形CFED,点P是线段BD上的一个动点,连接AP、PE,则使∠APE为直角的点P的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
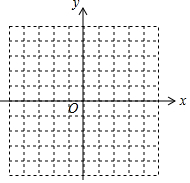 如图,在所给的平面直角坐标系中描出下列各点:①点A在x轴上方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度;②点B在x轴下方,y轴右侧,距离x、y轴都是3个单位长度;③点C在y轴上,位于原点下方,距离原点2个单位长度;④点D在x轴上,位于原点右侧,距离原点4个单位长度.
如图,在所给的平面直角坐标系中描出下列各点:①点A在x轴上方,y轴左侧,距离x轴4个单位长度,距离y轴2个单位长度;②点B在x轴下方,y轴右侧,距离x、y轴都是3个单位长度;③点C在y轴上,位于原点下方,距离原点2个单位长度;④点D在x轴上,位于原点右侧,距离原点4个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 美化城市,改善人居环境,已成为城市建设的一项重要内容,某市近几年通过抓旧房改造、植草、栽树、修建公园等措施,使城区绿化面积不断增大(如图所示).
美化城市,改善人居环境,已成为城市建设的一项重要内容,某市近几年通过抓旧房改造、植草、栽树、修建公园等措施,使城区绿化面积不断增大(如图所示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com