
分析 (1)把-25移到等号的右边,然后利用直接开平方法求解;
(2)把-5移到等号的右边,然后等号两边同时加上一次项一半的平方,再开方求解;
(3)直接利用平方差公式把方程左边分解因式,进而整理为两个一次因式的乘积,最后解一元一次方程即可;
(4)首先找出方程中a、b和c的值,求出△,进而代入求根公式求出方程的解.
解答 解:(1)∵(x+2)2-25=0,
∴(x+2)2=25,
∴x+2=±5,
∴x1=3,x2=-7;
(2)∵x2+4x-5=0,
∴x2+4x+4=9,
∴(x+2)2=9,
∴x+2=±3,
∴x1=-5,x2=1;
(3)∵4(x+3)2-(x-2)2=0,
∴[2(x+3)+(x-2)][2(x+3)-(x-2)]=0,
∴(3x+4)(x+8)=0,
∴3x+4=0或x+8=0,
∴x1=-$\frac{4}{3}$,x2=-8;
(4)∵a=2,b=8,c=-1,
∴△=b2-4ac=64+8=72,
∴x=$\frac{-8±\sqrt{72}}{2×2}$=$\frac{-4±3\sqrt{2}}{2}$,
∴x1=$\frac{-4+3\sqrt{2}}{2}$,x2=$\frac{-4-3\sqrt{2}}{2}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
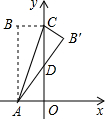 如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).
如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com