
| m |
| x |
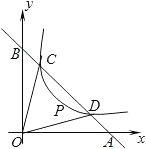 y1)、D(x2,y2),连接OC、OD(O是坐标有点),若∠BOC=∠AOD=α,且tanα=
y1)、D(x2,y2),连接OC、OD(O是坐标有点),若∠BOC=∠AOD=α,且tanα=| 1 |
| 3 |
| 10 |
| 1 |
| 3 |
| 10 |
| DH |
| OH |
| 1 |
| 3 |
| x2 |
| y2 |
| 1 |
| 3 |
| 3 |
| x |
| OG |
| CG |
| 1 |
| 3 |
| x2 |
| x1 |
| 1 |
| 3 |
| 10 |
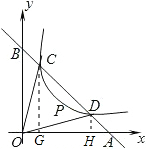
| DH |
| OH |
| 1 |
| 3 |
| y2 |
| x2 |
| 1 |
| 3 |
| 3 |
| x |
| 10 |


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
 最低成本是
最低成本是查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
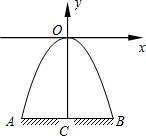 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:查看答案和解析>>
科目:初中数学 来源: 题型:
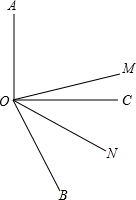 著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空.
著名数学教育家G.波利亚,有句名言:“发现问题比解决问题更重要”,这句话启发我们:要想学好数学,就需要观察,发现问题,探索问题的规律性东西,要有一双敏锐的眼睛.请先观察、计算再填空.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
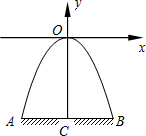 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com