
【题目】如图,在平面直角坐标系中,点A、C的坐标分别为(﹣1,0)、(0,﹣ ![]() ),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.
),点B在x轴上.已知某二次函数的图象经过A、B、C三点,且它的对称轴为直线x=1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交BC于点F.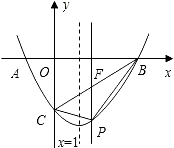
(1)求该二次函数的解析式;
(2)若设点P的横坐标为m,用含m的代数式表示线段PF的长;
(3)求△PBC面积的最大值,并求此时点P的坐标.
【答案】
(1)
解:设二次函数的解析式为y=ax2+bx+c(a≠0,a、b、c为常数),
由抛物线的对称性知B点坐标为(3,0),
依题意得:  ,
,
解得:  ,
,
∴所求二次函数的解析式为 ![]()
(2)
解:∵P点的横坐标为m,
∴P点的纵坐标为 ![]() ,
,
设直线BC的解析式为y=kx+b(k≠0,k、b是常数),
依题意,得 ![]() ,
,
∴  ,
,
故直线BC的解析式为 ![]() ,
,
∴点F的坐标为 ![]() ,
,
∴ ![]()
(3)
解:∵△PBC的面积 ![]()
![]() ,
,
∴当 ![]() 时,△PBC的最大面积为
时,△PBC的最大面积为 ![]() ,
,
把 ![]() 代入
代入 ![]() ,
,
得 ![]() ,
,
∴点P的坐标为 ![]()
【解析】此题文字比较多,而且图象也比较复杂,所以解题时需要理解题意.(1)可以采用待定系数法求二次函数的解析式,因为点A(﹣1,0)、C(0,﹣ ![]() )在函数图象上,对称轴为x=1,也可求得A的对称点B的坐标为(3,0),列方程组即可求得解析式;(2)先求得直线BC的解析式为
)在函数图象上,对称轴为x=1,也可求得A的对称点B的坐标为(3,0),列方程组即可求得解析式;(2)先求得直线BC的解析式为 ![]() ,则可求得点F的坐标为
,则可求得点F的坐标为 ![]() ,再求得点P的纵坐标为
,再求得点P的纵坐标为 ![]() ,可得线段PF的长;(3)利用面积和,△PBC的面积
,可得线段PF的长;(3)利用面积和,△PBC的面积 ![]() 即可求得.
即可求得.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,AB=6,点P是AB边上的任意一点(点P不与点A、点B重合),过点P作PD⊥AB,交直线BC于点D,作PE⊥AC,垂足为点F. 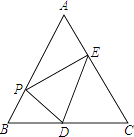
(1)求∠APE的度数;
(2)连接DE,当△PDE为等边三角形时,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
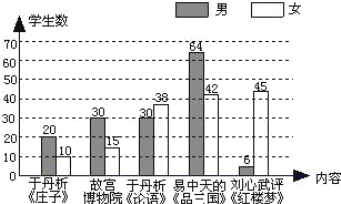
【题目】为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如下:
请根据统计图提供的信息回答以下问题:
(1)抽取的学生数为____名;
(2)该校有3000名学生,估计喜欢收听易中天《品三国》的学生有____名;
(3)估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的____%;
(4)你认为上述估计合理吗?理由是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实施新课改以来,某班学生经常采用“小组合作学习”的方式进行学习,值周班长对上周本班7个小组合作学习的得分情况进行了统计,得到以下评分结果:90,96,89,90,91,85,90,这组数据的中位数和众数分别是( )
A. 89,90B. 90,90C. 88,95D. 90,95
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com