
【题目】如图,四边形![]() 是菱形,且
是菱形,且![]() ,点
,点![]() 是对角线
是对角线![]() 上一点,
上一点,![]() ,绕点
,绕点![]() 逆时针旋转射线
逆时针旋转射线![]() ,旋转角度为
,旋转角度为![]() ,并交射线
,并交射线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,
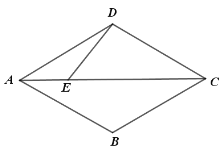
(1)①当![]() 时,补全图形,并证明
时,补全图形,并证明![]() ;
;
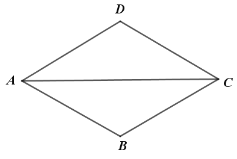
②当![]() 时,直接写出线段
时,直接写出线段![]() ,
,![]() ,
,![]() 之间的关系;
之间的关系;
(2)在平面上找到一点![]() ,使得对于任意的
,使得对于任意的![]() ,总有
,总有![]() ,直接写出点
,直接写出点![]() 的位置.
的位置.
(3)选择下面任意一问回答即可(全卷最多不超过100分)
A.证明(1)②的结论. | B.根据(2)中找到的 |
【答案】(1)①见解析;(1)②![]() ;(2)过点G作AG的垂线与AG绕点A顺时针针旋转的交点为k;(3)见解析
;(2)过点G作AG的垂线与AG绕点A顺时针针旋转的交点为k;(3)见解析
【解析】
(1)①连接EB,通过AAS证△CBE≌△EBG;
(1)②将ED转化为EB,EC转化为BG,在Rt△EGB中得到线段直角的关系;
(2)构造含30°的Rt△AGK,即可得到结论;
(3)前2问已证明
(1)①图形如下,连接BE
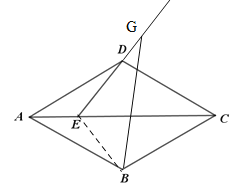
∵四边形ABCD是菱形,∠BAD=60°
∴∠DCE=∠BCE=30°
∵∠DEC=∠GBC =50°
∴根据菱形的对称性∠BEC=50°,
在△BCE中,
∴∠EBG=180°-∠BCE-∠GBC-∠BEC=50°=∠GEB
∴在△EDC中,∠EDC=100°
∴在四边形ADCB中,∠EBC=100°,∴∠BEC=∠EBG
∵BE=BE
∴△CBE≌△EBG
∴EG=BC
②![]()
(2)如下图,过点G作AG的垂线,交AC于点M,顺时针旋转AG至AK处,使得∠GAD=∠KAC,AK与GM的交点为点K
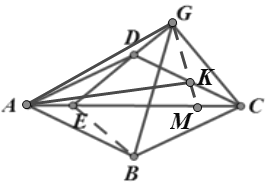
(3)A.
根据菱形的对称性,ED=EB,∠BEC=∠DEC=45°
∴∠GEB=90°,△GEB是直角三角形
∵∠BGE=∠BCE=30°,
则有EG=![]() ,
,
过B点作BH⊥CE于点H,
∵∠CEB=45°,∠ECB=30°,
∴![]()
![]()
∴![]()

B.
∵∠DAC=30°,∠GAD=∠KAC
∴∠GAK=30°
∵AG⊥GM
∴△AGK是直角三角形,且∠GAK=30°
∴![]()


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)若这种冰箱的售价降低50元,每天的利润是 元;
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到更多的实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时利润最高,并求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 轴的正半轴上),与
轴的正半轴上),与![]() 轴交于点
轴交于点![]() ,矩形
,矩形![]() 的一条边
的一条边![]() 在线段
在线段![]() 上,顶点
上,顶点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上.
上.

![]() 求点
求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
![]() 若点
若点![]() 的坐标为
的坐标为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
![]() 当矩形
当矩形![]() 的面积
的面积![]() 取最大值时,
取最大值时,
①求直线![]() 的解析式;
的解析式;
②在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,若点
,若点![]() 恰好落在该抛物线上,则
恰好落在该抛物线上,则![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
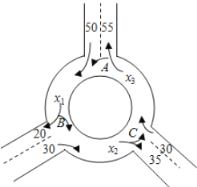
【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时段,单位时间进出口![]() ,
,![]() ,
,![]() 的机动车辆数如图所示,图中
的机动车辆数如图所示,图中![]() ,
,![]() ,
,![]() 分别表示该时段单位时间通过路段
分别表示该时段单位时间通过路段![]() ,
,![]() ,
,![]() 的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).
的机动车辆数(假设:单位时间内,在上述路段中,同一路段上驶入与驶出的车辆数相等).
(1)若![]() ,
,![]() __________.
__________.
(2)![]() 与
与![]() 的等量关系为__________.
的等量关系为__________.
(3)![]() ,
,![]() ,
,![]() 的大小关系为__________.(用>连接).
的大小关系为__________.(用>连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,B,与反比例函数图象的一个交点为
,B,与反比例函数图象的一个交点为![]() .
.
(1)求反比例函数的表达式;
(2)设直线![]() 与
与![]()
![]() 轴,
轴,![]() 轴分别交于点C,D,且
轴分别交于点C,D,且![]() ,直接写出
,直接写出![]() 的值 .
的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
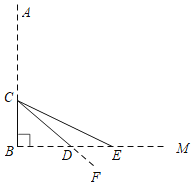
【题目】如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度.(精确到0.1m.参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() (点
(点![]() 的对应点分别是
的对应点分别是![]() ),射线
),射线![]() 分别交直线
分别交直线![]() 于点
于点![]() .
.
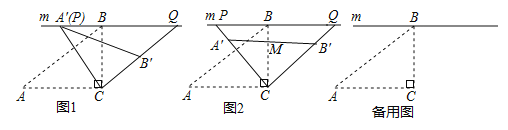
(1)问题发现:如图1所示,若![]() 与
与![]() 重合,则
重合,则![]() 的度数为_________________
的度数为_________________
(2)类比探究:如图2,所示,设![]() 与
与![]() 的交点为M,当M为
的交点为M,当M为![]() 中点时,求线段
中点时,求线段![]() 的长;
的长;
(3)拓展延伸:在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值,若存在,直接写出四边形
的面积是否存在最小值,若存在,直接写出四边形![]() 的最小面积;若不存在,请说明理由
的最小面积;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中AC,BD相交于点O,点E是OA的中点,连接BE并延长AD于点F,已知△AEF的面积=1,则平行四边形ABCD的面积是( )
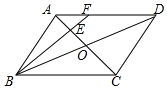
A.24B.18C.12D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com