
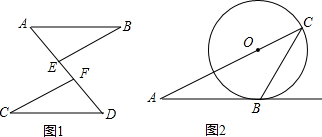
分析 (1)根据平行线的性质得出∠A=∠D,根据SAS推出△ABE≌△DCF,根据全等三角形的性质得出即可;
(2)连接OB,根据切线的性质求出∠OBA,求出∠AOB,根据三角形外角性质和等腰三角形的性质求出即可.
解答 (1)证明:∵AB∥CD,
∴∠A=∠D,
在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠D}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DCF(SAS),
∴∠B=∠C;
(2)解:连接OB,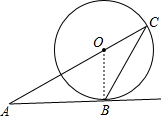
∵AB切⊙O于B,
∴∠OBA=90°,
∵∠A=26°,
∴∠AOB=180°-90°-26°=64°,
∵OB=OC,
∴∠C=∠OBC,
∴∠AOB=∠C+∠DBC=2∠ACB,
∴∠ACB=32°.
点评 本题考查了全等三角形的性质和判定和切线的性质的应用,能综合运用定理进行推理是解此题的关键,注意:圆的切线垂直于过切点的半径.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 销售价(元/条) |
| 羽绒被 | 415 |
| 羊毛被 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
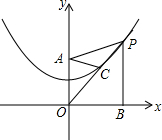 如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )
如图,点P是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的点,线段PO交抛物线于点C,PB⊥x轴于点B,点A的坐标是(0,2),当点C是OP的中点时,下列说法错误的是( )| A. | PA=PB | B. | ∠POB=45° | C. | PA=2AC | D. | PB=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x>-3}\\{x>2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<-3}\\{x<2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>-3}\\{x<2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x<-3}\\{x>2}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com