
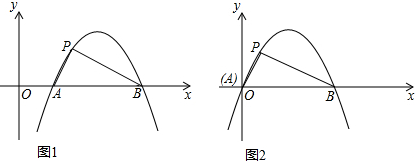
分析 (1)根据抛物线勾股点的定义即可得;
(2)作PG⊥x轴,由点P坐标求得AG=1、PG=$\sqrt{3}$、PA=2,由tan∠PAB=$\frac{PG}{AG}$=$\sqrt{3}$知∠PAG=60°,从而求得AB=4,即B(4,0),待定系数法求解可得;
(3)由S△ABQ=S△ABP且两三角形同底,可知点Q到x轴的距离为$\sqrt{3}$,据此求解可得.
解答 解:(1)抛物线y=-x2+1的勾股点的坐标为(0,1);
(2)抛物线y=ax2+bx过原点,即点A(0,0),
如图,作PG⊥x轴于点G,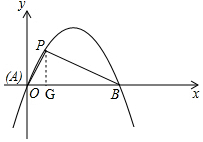
∵点P的坐标为(1,$\sqrt{3}$),
∴AG=1、PG=$\sqrt{3}$,PA=$\sqrt{A{G}^{2}+P{G}^{2}}$=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}$=2,
∵tan∠PAB=$\frac{PG}{AG}$=$\sqrt{3}$,
∴∠PAG=60°,
在Rt△PAB中,AB=$\frac{PA}{cos∠PAB}$=$\frac{2}{\frac{1}{2}}$=4,
∴点B坐标为(4,0),
设y=ax(x-4),
将点P(1,$\sqrt{3}$)代入得:a=-$\frac{\sqrt{3}}{3}$,
∴y=-$\frac{\sqrt{3}}{3}$x(x-4)=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x;
(3)①当点Q在x轴上方时,由S△ABQ=S△ABP知点Q的纵坐标为$\sqrt{3}$,
则有-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x=$\sqrt{3}$,
解得:x1=3,x2=1(不符合题意,舍去),
∴点Q的坐标为(3,$\sqrt{3}$);
②当点Q在x轴下方时,由S△ABQ=S△ABP知点Q的纵坐标为-$\sqrt{3}$,
则有-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x=-$\sqrt{3}$,
解得:x1=2+$\sqrt{7}$,x2=2-$\sqrt{7}$,
∴点Q的坐标为(2+$\sqrt{7}$,-$\sqrt{3}$)或(2-$\sqrt{7}$,-$\sqrt{3}$);
综上,满足条件的点Q有3个:(3,$\sqrt{3}$)或(2+$\sqrt{7}$,-$\sqrt{3}$)或(2-$\sqrt{7}$,-$\sqrt{3}$).
点评 本题主要考查抛物线与x轴的交点及待定系数法求函数解析式,根据新定义求得点B的坐标,并熟练掌握待定系数求函数解析式及三角形面积问题是解题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
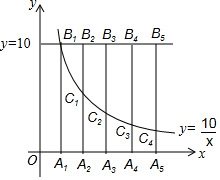 如图,直线y=10与反比例函数y=$\frac{10}{x}$( x>0)图象交于点B1,作A1B1⊥x轴,垂足为A1,在A1右侧依次取连续整数点,(横坐标为整数)A2,A3,A4,A5,过这些整数点分别作y轴的平行线交直线y=10于B2,B3,B4,B5,交反比例函数y=$\frac{10}{x}$(x>0)图象于点C1,C2,C3,C4.若B2C1=aA2C1,B3C2=bA3C2,B4C3=cA4C3,B5C4=dA5C4,则a+b+c+d的值为.
如图,直线y=10与反比例函数y=$\frac{10}{x}$( x>0)图象交于点B1,作A1B1⊥x轴,垂足为A1,在A1右侧依次取连续整数点,(横坐标为整数)A2,A3,A4,A5,过这些整数点分别作y轴的平行线交直线y=10于B2,B3,B4,B5,交反比例函数y=$\frac{10}{x}$(x>0)图象于点C1,C2,C3,C4.若B2C1=aA2C1,B3C2=bA3C2,B4C3=cA4C3,B5C4=dA5C4,则a+b+c+d的值为.| A. | 10 | B. | 8 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
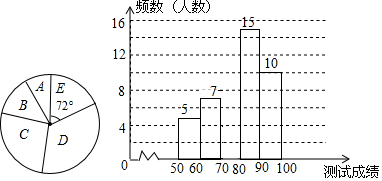
| 类别 | 成绩x分 | 频数(人数) |
| A | 50≤x<60 | 5 |
| B | 60≤x<70 | 7 |
| C | 70≤x<80 | a |
| D | 80≤x<90 | 15 |
| E | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
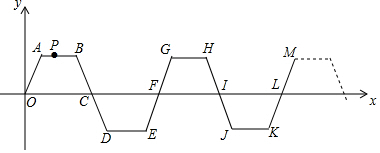
| A. | (1342,0) | B. | (1343,0) | C. | (1344,0) | D. | (1345,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
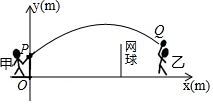 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.
甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式y=a(x-4)2+h,已知点O与球网的水平距离为5m,球网的高度为1.55m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.55354×105人 | B. | 5.5354×105人 | C. | 5.5354×104人 | D. | 55.354×103人 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com