
【题目】已知反比例函数y=﹣ ![]() 的图像和一次函数y=kx﹣1的图像都经过点P(m,﹣3m).
的图像和一次函数y=kx﹣1的图像都经过点P(m,﹣3m). 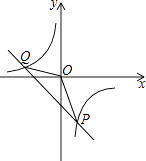
(1)求点P的坐标和这个一次函数的表达式;
(2)若这两个图像的另一个交点Q纵坐标为2,O为坐标原点,求△POQ的面积;
(3)若点M(a,y1)和点N(a+1,y2)都在这个反比例函数的图像上,比较y1和y2的大小.
【答案】
(1)解:∵反比例函数y=﹣ ![]() 的图像经过点P(m,﹣3m),
的图像经过点P(m,﹣3m),
∴﹣3m=﹣ ![]() ,
,
解得,m=1,
∴点P的坐标为(1,﹣3),
把点P的坐标为(1,﹣3)代入y=kx﹣1,
得,﹣3=k﹣1,
解得,k=﹣2,
∴一次函数的表达式为y=﹣2x﹣1
(2)解:当y=2时,﹣2x﹣1=2,
解得,x=﹣ ![]() ,
,
则点Q的坐标为(﹣ ![]() ,2),
,2),
设直线PQ与y轴的交点为M,则点M的坐标为(0,﹣1),
∴△POQ的面积=△MOQ的面积+△POM的面积= ![]() ×1×
×1× ![]() +
+ ![]() ×1×1=
×1×1= ![]()
(3)解:当a+1<0,即a<﹣1时,点M、N都在第二象限,
则y1<y2;
当a>0时,点M、N都在第四象限,
则y1<y2;
当﹣1<a<0时,y1>y2.
【解析】(1)把点P的坐标代入反比例函数的解析式求出m的值,得到点P的坐标,把点P的坐标代入一次函数解析式求出k;(2)根据题意求出点Q的坐标,利用三角形的面积公式计算即可;(3)分a<﹣1、a>0、﹣1<a<0三种情况,根据反比例函数的性质解答即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
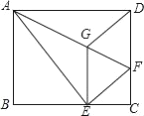
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF×AF;
GF×AF;
(3)若![]() ,折痕AF=5
,折痕AF=5![]() cm,则矩形ABCD的周长为 .
cm,则矩形ABCD的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滨州苏宁电器超市销售每台进价分别为190元、160元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1720元 |
第二周 | 4台 | 10台 | 2960 元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5100元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列各式分解因式时应提取的公因式:
(1)ax-ay应提取的公因式是________;
(2)3mx-6nx2应提取的公因式是__________;
(3)-x2+xy-xz应提取的公因式是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】坐标平面上有一点A,且点A到x轴的距离为3,点A到y轴的距离恰为点A到x轴距离的2倍.若点A在第二象限,则点A的坐标为( )
A. (-3,6) B. (-3,2) C. (-6,3) D. (-2,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.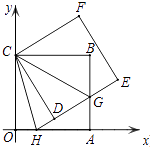
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,当G点在何位置时四边形AEBD是矩形?请说明理由并求出点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t , 估计当x=3.2千克时,t的值为( )
A.140
B.138
C.148
D.160
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AB=6.点D在AB边上,点E是BC边上一点(不与点B、C重合),且DA=DE,则AD的取值范围是 . 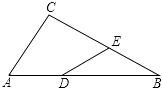
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com