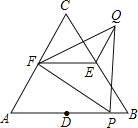
[题目]如图.△ABC和△FPQ均是等边三角形.点D.E.F分别是△ABC三边的中点.点P在AB边上.连接EF.QE．若AB=6.PB=1.则QE= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，△ABC和△FPQ均是等边三角形，点D、E、F分别是△ABC三边的中点，点P在AB边上，连接EF、QE．若AB=6，PB=1，则QE=　　．

【答案】2

【解析】

试题如图，连接FD，

∵△ABC为等边三角形，∴AC=AB=6，∠A=60°。

∵点D、E、F分别是等边△ABC三边的中点，AB=6，PB=1，

∴AD=BD=AF=3，DP=DB﹣PB=3﹣1=2，EF为△ABC的中位线。

∴EF∥AB，EF=AB=3，△ADF为等边三角形。∴∠FDA=60°，∴∠1+∠3=60°。

∵△PQF为等边三角形，∴∠2+∠3=60°，FP=FQ。∴∠1=∠2。

∵在△FDP和△FEQ中，FP=FQ，∠1=∠2，FD=FE，∴△FDP≌△FEQ（SAS）。∴DF=QE。

∵DF=2，∴QE=2。　

练习册系列答案

8年沉淀1年突破单元同步夺冠卷系列答案

导学与测试系列答案

成龙计划高效课时学案系列答案

超能学典名牌中学期末突破一卷通系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图1，在平面直角坐标系xOy中，线段AB在x轴的正半轴上移动,且AB=1，过点A、B作y轴的平行线分别交函数y1=(x>0)与y2=(x>0)的图像于C、E和D、F，设点A的横坐标为m (m>0).

（1）连接OC、OE，则△OCE面积为；

（2）连接CF，当m为何值时，四边形ABFC是矩形；

（3）连接CD、EF，判断四边形CDFE能否是平行四边形，并说明理由；

（4）如图2，经过点B和y轴上点G（0，4）作直线BG交直线AC于点H，若点H的纵坐标为正整数，请求出整数m的值.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】出租车司机张师傅某天上午营运全是在东西向的长江路上进行的，如果向东为正，向西为负，这天上午他行车里程（单位：km）如下：

⑴.最后一名乘客送到目的地，出租车在东面还是西面？在多少千米处？

⑵.请你帮张师傅算一下，这天上午他一共行驶了多少里程？

⑶.若每千米耗油0.1L，则这天上午张师傅一共用了多少升油？

查看答案和解析>>

科目：初中数学 来源： 题型：

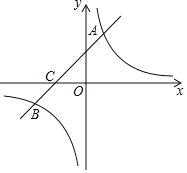
【题目】如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象相交于第一、三象限内的两点，与轴交于点 .

⑴求该反比例函数和一次函数的解析式；

⑵在轴上找一点使最大，求的最大值及点的坐标；

⑶直接写出当时，的取值范围.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图1，已知AB=AC，D为∠BAC的角平分线上面一点，连接BD，CD；如图2，已知AB=AC，D、E为∠BAC的角平分线上面两点，连接BD，CD，BE，CE；如图3，已知AB=AC，D、E、F为∠BAC的角平分线上面三点，连接BD，CD，BE，CE，BF，CF；…，依次规律，第n个图形中有全等三角形的对数是_________．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】解：根据算术平方根的意义，由，得(2x－y)2＝9，所以2x－y＝3．①(第一步)

根据立方根的意义，由，得x－2y＝－3．②(第二步)

解得x＝3，y＝3．

把x、y的值代入分式中，得．(第三步)

上述解答有两处错误，一处是___________步，忽视了___________；另一处是步___________，忽视了___________．请写出正确的解答过程．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】跃壮五金商店准备从宁云机械厂购进甲、乙两种零件进行销售．若每个甲种零件的进价比每个乙种零件的进价少2元，且用80元购进甲种零件的数量与用100元购进乙种零件的数量相同．

（1）求每个甲种零件、每个乙种零件的进价分别为多少元？

（2）若该五金商店本次购进甲种零件的数量比购进乙种零件的数量的3倍还少5个，购进两种零件的总数量不超过95个，该五金商店每个甲种零件的销售价格为12元，每个乙种零件的销售价格为15元，则将本次购进的甲、乙两种零件全部售出后，可使销售两种零件的总利润（利润＝售价－进价）超过371元，通过计算求出跃壮五金商店本次从宁云机械厂购进甲、乙两种零件有几种方案？请你设计出来．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系中, △ABC的三个顶点的位置如图所示，点A'的坐标是

（－2,2）, 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。