

·ÖĪö £Ø1£©øł¾Ż“ż¶ØĻµŹż·Ø£¬æɵĆŗÆŹż½āĪöŹ½£»
£Ø2£©øł¾ŻĘ½ŠŠÓŚyÖįµÄÖ±ĻßÉĻĮ½µć¼äµÄ¾ąĄėŹĒ½Ļ“óµÄׯ×ų±ź¼õ½ĻŠ”µÄׯ×ų±ź£¬æɵĆMEµÄ³¤£¬øł¾ŻČż½ĒŠĪµÄĆ껿£¬æɵƶž“ĪŗÆŹż£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ£¬æɵƓš°ø£®
£Ø3£©¼“æÉČ·¶Ø”÷BEP£¬øł¾ŻĻąĖĘČż½ĒŠĪµÄÅŠ¶Ø¶ØĄķ¼“æÉĒóµĆµćQµÄ×ų±ź£¬½āĢāŹ±ŅŖ×¢Ņā“š°øµÄ²»ĪØŅ»ŠŌ£®
½ā“š ½ā£ŗ£Ø1£©½«A”¢Gµć×ų±ź“śČėŗÆŹż½āĪöŹ½£¬µĆ
$\left\{\begin{array}{l}{9a+3b+3\sqrt{3}=0}\\{a-b+3\sqrt{3}=0}\end{array}\right.$£¬
½āµĆ$\left\{\begin{array}{l}{a=-\sqrt{3}}\\{b=2\sqrt{3}}\end{array}\right.$£¬
Å×ĪļĻߵĽāĪöŹ½ĪŖy=-$\sqrt{3}$x2+2$\sqrt{3}$x+3$\sqrt{3}$£»
£Ø2£©×÷ME”ĶxÖį½»ABÓŚEµć£¬ČēĶ¼1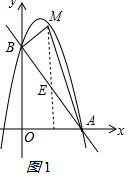 £¬
£¬
µ±x=0Ź±£¬y=3$\sqrt{3}$£¬¼“Bµć×ų±źĪŖ£Ø0£¬3$\sqrt{3}$£©
Ö±ĻßABµÄ½āĪöŹ½ĪŖy=-$\sqrt{3}$x+3$\sqrt{3}$£¬
ÉčM£Øn£¬-$\sqrt{3}$n2+2$\sqrt{3}$n+3$\sqrt{3}$£©£¬E£Øn£¬-$\sqrt{3}$n+3$\sqrt{3}$£©£¬
MEØT-$\sqrt{3}$n2+2$\sqrt{3}$n+3$\sqrt{3}$-£Ø-$\sqrt{3}$n+3$\sqrt{3}$£©=-$\sqrt{3}$n2+5$\sqrt{3}$n£¬
S”÷ABM=$\frac{1}{2}$ME•xA=$\frac{1}{2}$£Ø-$\sqrt{3}$n2+5$\sqrt{3}$n£©”Į3=-$\frac{3\sqrt{3}}{2}$£Øn-$\frac{5}{2}$£©2+$\frac{75\sqrt{3}}{8}$£¬
µ±n=$\frac{5}{2}$Ź±£¬”÷ABMĆ껿µÄ×ī“óÖµŹĒ$\frac{75\sqrt{3}}{8}$£»
£Ø3£©“ęŌŚ£»ĄķÓÉČēĻĀ£ŗ
OE=$\frac{2\sqrt{3}}{3}$£¬AP=2£¬OP=1£¬BE=3$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$=$\frac{7\sqrt{3}}{3}$£¬
µ±y=$\frac{2\sqrt{3}}{3}$Ź±£¬-$\sqrt{3}$x+3$\sqrt{3}$=$\frac{2\sqrt{3}}{3}$£¬½āµĆx=$\frac{7}{3}$£¬¼“EF=$\frac{7}{3}$
½«”÷BEPČʵćEĖ³Ź±Õė·½ĻņŠż×Ŗ90”ć£¬µĆµ½”÷B'EC£ØČēĶ¼3£©£¬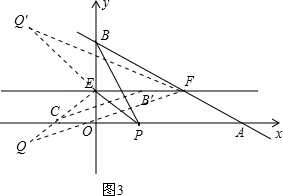
”ßOB”ĶEF£¬
”ąµćB'ŌŚÖ±ĻßEFÉĻ£¬
”ßCµćŗį×ų±ź¾ų¶ŌÖµµČÓŚEO³¤¶Č£¬Cµćׯ×ų±ź¾ų¶ŌÖµµČÓŚEO-PO³¤¶Č£¬
”ąCµć×ų±źĪŖ£Ø-$\frac{2\sqrt{3}}{3}$£¬$\frac{2\sqrt{3}}{3}$-1£©£¬
¹żF×÷FQ”ĪB'C£¬½»ECÓŚµćQ£¬
Ōņ”÷FEQ”×”÷B'EC£¬
ÓÉ$\frac{BE}{EF}$=$\frac{B”äE}{EF}$=$\frac{CE}{EQ}$=$\sqrt{3}$£¬
æɵĆQµÄ×ų±źĪŖ£Ø-$\frac{2}{3}$£¬-$\frac{\sqrt{3}}{3}$£©£»
øł¾Ż¶Ō³ĘŠŌæÉµĆ£¬Q¹ŲÓŚÖ±ĻßEFµÄ¶Ō³ĘµćQ'£Ø-$\frac{2}{3}$£¬$\frac{5\sqrt{3}}{3}$£©Ņ²·ūŗĻĢõ¼ž£®
µćĘĄ ±¾Ģāæ¼²éĮĖ¶ž“ĪŗÆŹż×ŪŗĻĢā£¬½ā£Ø1£©µÄ¹Ų¼üŹĒ“ż¶ØĻµŹż·Ø£»½ā£Ø2£©µÄ¹Ų¼üŹĒĄūÓĆČż½ĒŠĪµÄĆ껿µĆ³ö¶ž“ĪŗÆŹż£»½ā£Ø3£©µÄ¹Ų¼üŹĒĻąĖĘČż½ĒŠĪµÄÅŠ¶ØÓėŠŌÖŹ£¬ŹżŠĪ½įŗĻĖ¼ĻėµÄÓ¦ÓĆ£¬»¹ŅŖ×¢Ņā“š°øµÄ²»ĪØŅ»ŠŌ£¬²»ŅŖĀ©½ā£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
 ČēĶ¼£¬ŌŚÖ±½Ē×ų±źĘ½ĆęÄŚ£¬”÷ABCµÄ¶„µćA£Ø-1£¬0£©£¬µćBÓėµćA¹ŲÓŚŌµć¶Ō³Ę£¬AB=BC£¬”ĻCAB=30”ć£¬½«”÷ABCČʵćCŠż×Ŗ£¬Ź¹µćAĀäŌŚxÖįÉĻµÄµćD“¦£¬µćBĀäŌŚµćE“¦£¬ÄĒĆ“BEĖłŌŚÖ±ĻߵĽāĪöŹ½ĪŖy=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$£®
ČēĶ¼£¬ŌŚÖ±½Ē×ų±źĘ½ĆęÄŚ£¬”÷ABCµÄ¶„µćA£Ø-1£¬0£©£¬µćBÓėµćA¹ŲÓŚŌµć¶Ō³Ę£¬AB=BC£¬”ĻCAB=30”ć£¬½«”÷ABCČʵćCŠż×Ŗ£¬Ź¹µćAĀäŌŚxÖįÉĻµÄµćD“¦£¬µćBĀäŌŚµćE“¦£¬ÄĒĆ“BEĖłŌŚÖ±ĻߵĽāĪöŹ½ĪŖy=$\frac{\sqrt{3}}{3}$x-$\frac{\sqrt{3}}{3}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | a-3£¾b-3 | B£® | $\frac{1}{2}$a£¼$\frac{1}{2}$b | C£® | a-b£¼0 | D£® | -3a£¾-3b |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

| °×Ö½ÕÅŹż | 1 | 2 | 3 | 4 | 5 | ” |
| Ö½Ģõ³¤¶Č | 40 | 75 | 110 | 145 | 180 | ” |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 30”ć | B£® | 60”ć | C£® | 90”ć | D£® | 120”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® |  | B£® |  | C£® |  | D£® |  |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com