练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，三角形ABC内部有若干个点，用这些点以及三角形ABC的顶点A、B、C把原三角形分割成一些小的三角形（互相不重叠）：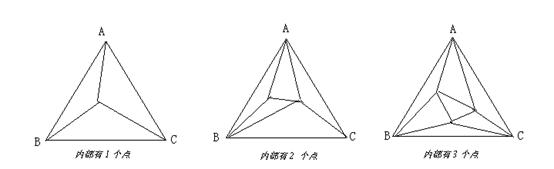

    填写下表：

    （2）原三角形能否被分割成2013个小三角形？若能，求此时三角形ABC内部有多少个点？若不能，请说明理由。

    （1）由题意得

    三角形ABC内点的个数
    		1
    		2
    		3
    		4
    		…

    分割成的三角形的个数
    		3
    		5
    		7
    		9
    		…
    		2n+1
    （2）能，1006.

    解析试题分析：（1）观察图形，不难发现：内部每多一个点，则多2个三角形，则易得到；
    （2）根据（1）的结论，列方程求解即可．
    （1）由题意得

    三角形ABC内点的个数
    		1
    		2
    		3
    		4
    		…

    分割成的三角形的个数
    		3
    		5
    		7
    		9
    		…
    		2n+1
    （2）由题意得，解得
    所以原三角形能被分割成2013个小三角形，此时三角形ABC内部有1006个点.
    考点：找规律-图形的变化
    点评：解答此类问题的关键是读懂题意及图形特征找到规律，再把这个规律应用于解题.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图：三角形ABC内接于圆O，∠BAC与∠ABC的角平分线AE，BE相交于点E，延长AE交外接圆O精英家教网于点D，连接BD，DC，且∠BCA=60°
    （1）求∠BED的大小；
    （2）证明：△BED为等边三角形；
    （3）若∠ADC=30°，圆O的半径为r，求等边三角形BED的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图，三角形ABC内接于⊙O，AB为直径，过点A作直线EF，要使得EF是⊙O的切线，还需添加的条件是（只需写出三种）：①
    OA⊥EF
    OA⊥EF
    或②
    ∠FAC=∠B
    ∠FAC=∠B
    或③
    ∠BAC+∠FAC=90°
    ∠BAC+∠FAC=90°
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，三角形ABC内的线段BD、CE相交于点0．已知OB=OD，OC=20E，设三角形BOE、三角形BOC、三角形COD和四边形AEOD的面积分别为S1、S2、S3、S4．
    （1）求S1：S3的值．
    （2）如果S2=2，求S4的值．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，三角形ABC内的线段BD、CE相交于点0．已知OB=OD，OC=20E，设三角形BOE、三角形BOC、三角形COD和四边形AEOD的面积分别为S1、S2、S3、S4．
    （1）求S1：S3的值．
    （2）如果S2=2，求S4的值．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源：2008年浙江省杭州市外国语学校初中直升高中选拔数学试卷（解析版） 题型：解答题

    如图：三角形ABC内接于圆O，∠BAC与∠ABC的角平分线AE，BE相交于点E，延长AE交外接圆O于点D，连接BD，DC，且∠BCA=60°
    （1）求∠BED的大小；
    （2）证明：△BED为等边三角形；
    （3）若∠ADC=30°，圆O的半径为r，求等边三角形BED的边长．

    查看答案和解析>>

    同步练习册答案