
 已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右作正方形CDEF,连结BF.若S△OBC=8,AC=BC.
已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B两点,与y轴交于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右作正方形CDEF,连结BF.若S△OBC=8,AC=BC.分析 (1)根据抛物线的对称性得到抛物线的对称轴为y轴,则b=0;然后利用方程与二次函数的关系求得点B、C的坐标,由S△OBC=8可以求得c的值;
(2)由抛物线y=-$\frac{1}{4}$x2+4交x轴于点A、B,当x=0,求出图象与y轴的交点坐标,以及y=0,求出图象与x轴的交点坐标,即可得出三角形的形状;首先证明△ACD≌△BCF,利用三角形的全等,得出∠ABF=∠ABC+∠CBF=90°,即可得出答案;
(3)由(2)知,点E在定直线上,当点D沿x轴正方向移动到点B时,点E所走过的路程长等于BC的长度.
解答 解:(1)由AC=BC,可知此抛物线的对称轴是y轴,
即b=0,
所以C(0,c)、B($\sqrt{4c}$,0),
由S△OBC=$\frac{1}{2}$×OB×OC=8,
得c=4,
抛物线解析式为y=-$\frac{1}{4}$x2+4;
(2)BF⊥AB,
理由:由(1)得C(0,4)、B(4,0),
所以∠ACB=2∠OCB=2×45°=90°,
在△ADC和△BFC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCF}\\{CD=CF}\end{array}\right.$,
∴△ADC≌△BFC(SAS),
∴∠FBC=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;
(3)作EM⊥x轴,交x轴于点M,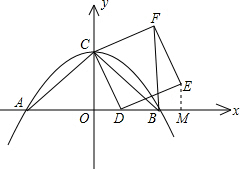 ∵∠ODC+∠EDM=90°,∠MDE+∠DEM=90°,
∵∠ODC+∠EDM=90°,∠MDE+∠DEM=90°,
∴∠ODC=∠DEM,
在△ODC和△MED中
$\left\{\begin{array}{l}{∠COD=∠DNE}\\{∠ODC=∠DEM}\\{CD=DE}\end{array}\right.$
∴△ODC≌△MED(AAS),
∴DM=OC=4,OD=EM,
又∵OD=OB-BD=4-BD=DM-BD=BM,
∴BM=EM,
∵∠FMB=90°,
∴∠MBE=∠MEB=45°,
∴∠FBE=45°,
∴点E所走过的路线长等于BC=4$\sqrt{2}$.
点评 本题考查了待定系数法求二次函数解析式、全等三角形的判定与性质、正方形和等腰直角三角形的性质,综合性强,考查学生数形结合的数学思想方法.(3)中弄清点E所走过的路程是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
 在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:
在无锡全民健身越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.下列四种说法:| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
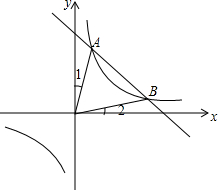 如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).
如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
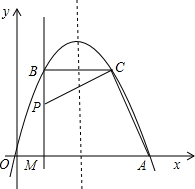 如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.
如图,经过原点的抛物线y=-x2+mx(m>2)与x轴的另一交点为A,过点P(1,$\frac{m}{2}$)作直线PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连接CB,CP,CA,要使得CA⊥CP,则m的值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
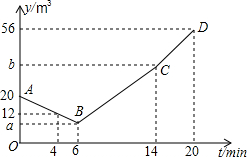 水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.| 时间 | 池中有水(m3) |
| 12:00 | 20 |
| 12:04 | 12 |
| 12:06 | a |
| 12:14 | b |
| 12:20 | 56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y3<y1<y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com