
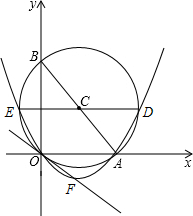
 ��ֱ������ϵ�У���C��ԭ��O����x���ڵ�A��2��0������y���ڵ�B��0��$2\sqrt{3}$����
��ֱ������ϵ�У���C��ԭ��O����x���ڵ�A��2��0������y���ڵ�B��0��$2\sqrt{3}$�������� ��1����ͼ�߶�AB��ԲC��ֱ������Ϊ��A��B��������֪������ƽ���ߵ����ʼ�����õ�C�����ꣻ
��2����Ϊ�����߹���A��O�����Կ���öԳ��ᣬ���������ֱ��y=-$\frac{\sqrt{3}}{3}$x�Ľ��㣬���Ƕ��κ����Ķ������꣬���ö���ʽ����һ��ʽ�����ô���ϵ����������������ߵĽ���ʽ��
��3����ΪDE��x�ᣬ�ҹ���C�����Կɵ�D��E��������Ϊ $\sqrt{3}$�����ֱ��AB�ij����ɵ�D��E�ĺ����꣬�������ʽ�����жϣ�
��4����ΪABΪֱ�������Ե��������ϵĵ�P�ڡ�C���ڲ�ʱ�������APBΪ�۽ǣ�����-1��x0��0����2��x0��3��
��� �⣺��1���ߡ�C����ԭ��O
��ABΪ��C��ֱ��
��CΪAB���е�
����C��CH��ֱx���ڵ�H������CH=$\frac{1}{2}$OB=$\sqrt{3}$��OH=$\frac{1}{2}$OA=1
��Բ��C������Ϊ��1��$\sqrt{3}$����
��2���������߹�O��A���㣬
�������ߵĶԳ���Ϊx=1��
�������ߵĶ�����ֱ��y=-$\frac{\sqrt{3}}{3}$x�ϣ�
�ඥ������Ϊ��1��-$\frac{\sqrt{3}}{3}$����
����������������������y=ax2+bx+c���� $\left\{\begin{array}{l}{c=0}\\{4a+2b+c=0}\\{a+b+c=-\frac{\sqrt{3}}{3}}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=-\frac{2\sqrt{3}}{3}}\\{c=O}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x��
��3����OA=2��OB=2$\sqrt{3}$��
��AB=$\sqrt{{2}^{2}+��2\sqrt{3}��^{2}}$=4������C�İ뾶r=2��
��D��3��$\sqrt{3}$����E��-1��$\sqrt{3}$����
����y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x���飬֪��D��E�����������ϣ�
��4����ABΪֱ����
�൱�������ϵĵ�P�ڡ�C���ڲ�ʱ�������APBΪ�۽ǣ�
��-1��x0��0����2��x0��3��
���� ���⿼����Բ����κ������ۺ�֪ʶ�������˴���ϵ������������Բ�����ʣ������˶��κ����ĶԳ��Եȣ�����Ĺؼ������ν��˼���Ӧ�ã��ۺ��ԱȽ�ǿ�������п�ѹ���⣮��


 ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �����¶�x���棩 | �� | 0 | 5 | 10 | 15 | 20 | 25 | �� |
| �����¶�y���H�� | �� | 32 | 41 | 50 | 59 | 68 | 77 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������������������� | |
| B�� | �������������Ҹ�ָ�� | |
| C�� | ���������������ճ�����֧����� | |
| D�� | ���������ijУ�༶ѧ���ԡ��������С���֪���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | -2 | C�� | -4 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com