练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】五一前夕，某时装店老板到厂家选购两种品牌的时装，若购进品牌的时装套，品牌的时装套，需要元；若购进品牌的时装套，品牌的时装套，需要元．

    (1)求两种品牌的时装每套进价分别为多少元？

    (2)若套品牌的时装售价元，套品牌的时装售价元，时装店将购进的两种时装共套全部售出，所获利润要不少于元，问品牌时装至少购进多少套？

    【答案】(1) 两种品牌的时装每套进价分别为元、元； (2) 至少购进品牌时装套

    【解析】

    （1）设两种品牌的时装每套进价分别为元，元，再根据题意列出关于x，y的二元一次方程组进行求解即可；

    （2）设品牌的时装购进套，根据“所获利润要不少于元，”列出关于m的不等式求解即可.

    解：设两种品牌的时装每套进价分别为元，元，

    ，

    解得

    答：两种品牌的时装每套进价分别为元，元；

    设品牌的时装购进套，则B品牌的时装购进（50﹣m）套，

    ，

    解得：，

    答：少购进品牌时装套.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

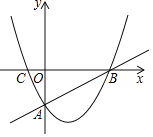
    【题目】如图，直线y＝x﹣2与x轴交于点B，与y轴交于点A，抛物线y＝ax2﹣x+c经过A，B两点，与x轴的另一交点为C．

    （1）求抛物线的解析式；

    （2）M为抛物线上一点，直线AM与x轴交于点N，当时，求点M的坐标；

    （3）P为抛物线上的动点，连接AP，当∠PAB与△AOB的一个内角相等时，直接写出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，过⊙T（半径为r）外一点P引它的一条切线，切点为Q，若0＜PQ≤2r，则称点P为⊙T的伴随点．

    （1）当⊙O的半径为1时，

    ①在点A(4，0)，B(0，)，C(1，)中，⊙O的伴随点是　 　；

    ②点D在直线y＝x+3上，且点D是⊙O的伴随点，求点D的横坐标d的取值范围；

    （2）⊙M的圆心为M(m，0)，半径为2，直线y＝2x﹣2与x轴，y轴分别交于点E，F．若线段EF上的所有点都是⊙M的伴随点，直接写出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

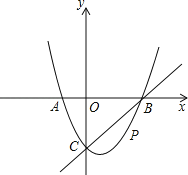
    【题目】如图，在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．

    （1）分别求出图中直线和抛物线的函数表达式；

    （2）连接PO、PC，并把△POC沿C O翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，(为坐标原点，点，点是中点，连接(将绕点顺时针旋转，得到,记旋转角为，点的对应点分别是,连接是中点，连接．

    （1）如图①，当时，求点的坐标；

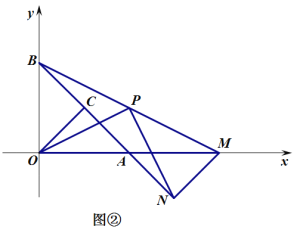
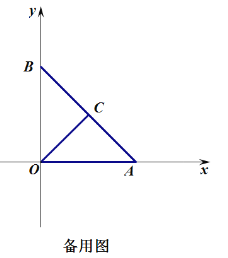
    （2）如图②，当时，求证，且；

    （3）当旋转至点共线时，求点的坐标(直接写出结果即可) ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两家商场平时以同样的价格出售相同的商品.“五一”节期间两家商场都让利酬宾.在甲商场按累计购物金额的收费；在乙商场累计购物金额超过元后，超出元的部分按收费．设小红在同一商场累计购物金额为元，其中．

    （1）根据题意，填写下表(单位：元)：

    累计购物金额

    ···

    在甲商场实际花费

    ···

    在乙商场实际花费

    ···

    （2）设小红在甲商场实际花费元，在乙商场实际花费元，分别求关于的函数解析式；

    （3）“五一”节期间小红如何选择这两家商场去购物更省钱？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

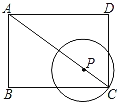
    【题目】如图，在矩形ABCD中，AB＝3，BC＝4，P是对角线AC上的动点，以点P为圆心，PC长为半径作⊙P．当⊙P与矩形ABCD的边相切时，CP的长为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+a+2(a≠0)与x轴交于点A(x1，0)，点B(x2，0)，(点A在点B的左侧)，抛物线的对称轴为直线x=-1．

    (1)若点A的坐标为(-3，0)，求抛物线的表达式及点B的坐标；

    (2)C是第三象限的点，且点C的横坐标为-2，若抛物线恰好经过点C，直接写出x2的取值范围；

    (3)抛物线的对称轴与x轴交于点D，点P在抛物线上，且∠DOP=45°，若抛物线上满足条件的点P恰有4个，结合图象，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l与⊙O相离，OA⊥l于点A，与⊙O相交于点P，OA＝5．C是直线l上一点，连接CP并延长，交⊙O于点B，且AB＝AC．

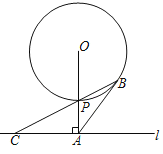
    （1）求证：AB是⊙O的切线；

    （2）若tan∠ACB＝，求线段BP的长．

    查看答案和解析>>

    同步练习册答案