
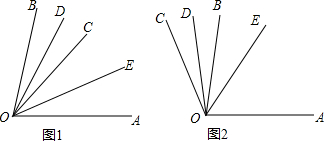
 已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.
已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.分析 (1)利用角平分线定义,求证∠DOE=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC,然后根据∠AOB=60°即可求出∠DOE的度数;
(2)利用角平分线定义,求证∠DOE=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC,然后根据∠AOB=60°即可求出∠DOE的度数;
(3)解题思路同(2),但是题干没有给图,所以需分类讨论,不要漏解.
解答 解:(1)∵OD、OE分别是∠BOC和∠COA的平分线,
∴∠COD=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠DOE=∠COD+∠COE=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOB=40°;
(2)∵OD、OE分别是∠BOC和∠COA的平分线,
∴∠COD=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
又∵∠AOB=80°,
∴∠DOE=∠COE-∠COD=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC=$\frac{1}{2}$∠AOB=40°.
(3)OD,OE在OA同侧.
∵OD、OE分别是∠BOC和∠COA的平分线,
∴∠COD=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠DOE=∠COD+∠COE=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOB=40°;
OD,OE在OA异侧.
∵OD、OE分别是∠BOC和∠COA的平分线,
∴∠COD=$\frac{1}{2}$∠BOC,∠COE=$\frac{1}{2}$∠AOC,
∴∠DOE=∠COD+∠COE=180°-$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC=$\frac{1}{2}$∠AOB=140°;
综上所述,∠DOE的度数是40°(OD,OE在OA同侧)或140°(OD,OE在OA异侧).
点评 此题主要考查学生对角的计算和角平分线定义的理解和掌握,对于学生来说此题有一定的拔高难度,属于中档题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
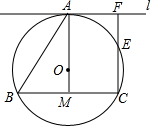 过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,
过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com