
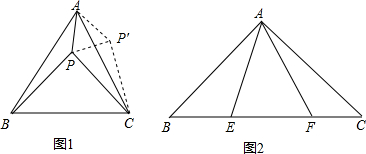
 如图,D、E分别是BC、AC的中点,BF平分∠ABC交DE于点F,若BC=6,AB=8,则EF的长是1.
如图,D、E分别是BC、AC的中点,BF平分∠ABC交DE于点F,若BC=6,AB=8,则EF的长是1.  黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
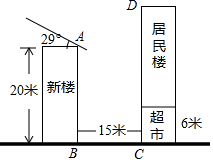 某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)
某居民小区有一朝向为正南方向的居民楼.该居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为29°.(参考数据:sin29°≈0.48;cos29°≈0.87;tan29°≈0.55)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=1 | B. | $x=\frac{7}{11}$ | C. | $x=\frac{11}{7}$ | D. | x=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7.
在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
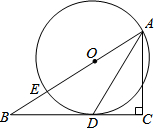 如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com