
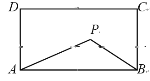
【题目】如图,在矩形ABCD中,AB=6,AD=3,动点P满足S△PAB=![]() S矩形ABCD,则点P到A、B两点间距离之和PA+PB的最小值为( )
S矩形ABCD,则点P到A、B两点间距离之和PA+PB的最小值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,∠AOB为锐角,在射线OA上依次截取A1A2=A2A3=A3A4=…=AnAn+1,在射线OB上依次截取B1B2=B2B3=B3B4=…=BnBn+1,记Sn为△AnBnBn+1的面积(n为正整数),若S3=7,S4=10,则S2019=( )
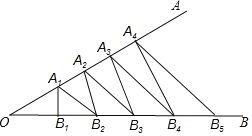
A.4039B.4041C.6055D.6058
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“作已知角的角平分线”的尺规作图过程.
已知:如图,∠AOB.
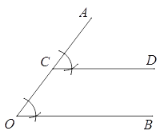
求作:∠AOB的角平分线OP.
作法:如图,
①在射线OA上任取点C;
②作∠ACD=∠AOB;
③以点C为圆心CO长为半径画圆,交射线CD于点P;
④作射线OP;
所以射线OP即为所求.
根据小元设计的尺规作图过程,完成以下任务.
(1)补全图形;
(2)完成下面的证明:
证明:∵ ∠ACD=∠AOB,
∴ CD∥OB(____________)(填推理的依据).
∴∠BOP=∠CPO.
又∵ OC=CP,
∴∠COP=∠CPO(____________)(填推理的依据).
∴∠COP=∠BOP.
∴ OP平分∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工人师傅用一块长为10dm,宽为6dm的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形.(厚度不计)

(1)在图中画出裁剪示意图,用实线表示裁剪线,虚线表示折痕;并求长方体底面面积为12dm2时,裁掉的正方形边长多大?
(2)若要求制作的长方体的底面长不大于底面宽的五倍,并将容器进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形边长多大时,总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,点
,点![]() 是弧
是弧![]() 上的任一点,过点
上的任一点,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() .连接
.连接![]() 交
交![]() 于
于![]() .
.
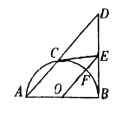
(1)求证:![]() ;
;
(2)填空:①当![]() _____时,四边形
_____时,四边形![]() 是正方形;
是正方形;
②当![]() _____时,四边形
_____时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com