
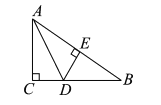
【题目】如图,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AC=3cm,BC=5cm,则三角形BDE的周长是_________________
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】对于正整数![]() ,定义
,定义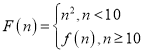 ,其中
,其中![]() 表示
表示![]() 的首位数字、末位数字的平方和.例如:
的首位数字、末位数字的平方和.例如:![]() ,
,![]() .规定
.规定![]() ,
,![]() (
(![]() 为正整数),例如,
为正整数),例如,![]() ,
,![]() .按此定义,则由
.按此定义,则由![]() __________,
__________,![]() ___________.
___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
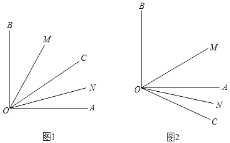
【题目】已知∠AOB=90°,OC是一条可以绕点O转动的射线,ON平分∠AOC,OM平分∠BOC.
(1)当射线OC转动到∠AOB的内部时,如图(1),求∠MON得度数.
(2)当射线OC转动到∠AOB的外时(90°<∠BOC<∠180°),如图2,∠MON的大小是否发生变化,变或者不变均说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过B作BE⊥CD,垂足为点E,连接AE,F为AE上一点,且∠BFE=∠C.
(1)求证:△ABF∽△EAD;
(2)若AB=4,∠BAE=30°,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.

请你结合这些算式,解答下列问题:
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n–1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,图2是点F运动时,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A. ![]() B. 2 C.
B. 2 C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判定中,正确的个数有( )
①一组对边平行,一组对边相等的四边形是平行四边形;
②对角线互相平分且相等的四边形是矩形;
③对角线互相垂直的四边形是菱形;
④对角线互相垂直平分且相等的四边形是正方形,
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com