
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作▱ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;(2)若BD=CD,求证:四边形ADCE是矩形.
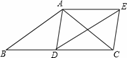
解答: 证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
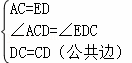 ,
,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD;
又∵BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三合一”性质),
∴∠ADC=90°,
∴▱ADCE是矩形.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
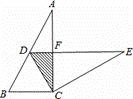
如图,在Rt△ABC 中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( )
A. 30,2 B. 60,2 C. 60,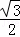 D. 60,
D. 60,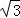
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示的圆柱体中底面圆的半径是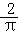 ,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 _________ .(结果保留根号)
,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 _________ .(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com