练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．am+bn=5，an-bm=4，则（a2+b2）（m2+n2）=41．

    分析 将已知两等式分别平方后可得a2m2+2abmn+b2n2=25 ①，a2n2-2abmn+b2m2=16 ②，①+②得a2m2+b2n2+a2n2+b2m2=41，等式左边因式分解即可得答案．

    解答 解：∵am+bn=5，an-bm=4，
    ∴（am+bn）2=25，即a2m2+2abmn+b2n2=25 ①，
    （an-bm）2=16，即a2n2-2abmn+b2m2=16 ②，
    ∴①+②，得：a2m2+b2n2+a2n2+b2m2=41，
    ∴a2（m2+n2）+b2（m2+n2）=41，
    ∴（a2+b2）（m2+n2）=41，
    故答案为：41．

    点评 本题主要考查多项式乘多项式与因式分解，根据已知条件得出待求代数式与已知等式间的联系是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    17．数轴上A点表示的数是1.5，则数轴上与A点相距3个单位长度的B点表示的数是4.5或-1.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

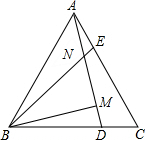    18．已知：△ABC为等边三角形，点D、E分别在BC和AC上，并且CD=AE，连接AD、BE相交于点N，过点B作BM⊥AD于点M．
    （1）求证：BE=AD；
    （2）若NE=1.6，MN=2，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．单项式与多项式相乘．结果仍是多项式，结果的项数等于多项式的项数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某商人如果将进货价为8元的商品按每件10元出售，每天可销售100件，现采用提高售出价，减少进货量的办法增加利润，已知这种商品每涨价1元其销售量就要减少10件，
    （1）求该商品平均每天的利润y（元）与售价x（元）之间的函数关系式；
    （2）问他将售出价定为多少元时，才能使每天所赚的利润最大？并求出最大利润；
    （3）若每件商品的售价不高于13元，那么将售价定为多少元时，可以获最大利润？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若2m+6n=5，则4m×64n=32．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．若x+2y=-6，则12-2x-4y=24．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图1，△ABC中，AB=AC，∠BAC=90°，点M是BC边上的一个动点，点B关于点M的对称点N在BC上（运动开始时，点M与点B重合，当点N到达点C时运动终止），过点M、N作BC的垂线，与折线B→A→C分别交于P、Q两点，设线段BM的长为x，四边形PQNM的面积为S，S关于x的函数图象如图2所示（其中0＜x≤$\frac{3}{2}$，$\frac{3}{2}$＜x≤a时，函数的解析式不同）．
    （1）填空：当PM=QN时，x的值为2；
    （2）求S关于x的函数关系式，并写出x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

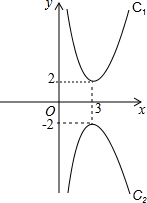    4．如图，在同一平面直角坐标系中，画出抛物线C1：y=（x-3）2+2和它关于x轴对称的抛物线C2，我们容易发现，抛物线C2的开口向下，形状与抛物线C1相同，其解析式是y=-（x-3）2-2，请运用轴对称的知识，求出抛物线C1关于y轴对称的抛物线C3的解析式．

    查看答案和解析>>

    同步练习册答案